
【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 ![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 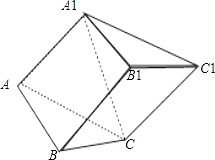
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小.
【答案】
(1)解:因为侧面A1ACC1⊥底面ABC,AA1侧面A1ACC1,
侧面A1ACC1∩底面ABC=AC
所以直线AA1在底面ABC内的射影为直线AC
故∠A1AC为侧棱AA1与底面ABC所成的角
又AA1⊥A1C,AA1=A1C,
所以∠A1AC=45°为所求.
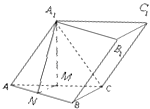
(2)解:取AC,AB的中点分别为M,N,连结A1M,MN,NA1
由(1)知A1M⊥AC,
故A1M⊥底面ABC,A1M⊥AB
又MN∥BC,∠ABC=90°
所以MN⊥AB,又MN∩A1M=M,所以AB⊥平面A1MN
则∠A1NM即为所求二面角的平面角
在RtA1MN中,A1M= ![]() ,AC=3,MN=
,AC=3,MN= ![]() BC=1,∠A1MN=90°,
BC=1,∠A1MN=90°,
所以tan∠A1MN= ![]() =3,∠A1MN=arctan3.
=3,∠A1MN=arctan3.
即所求二面角的大小为arctan3.
【解析】(1)由已知得直线AA1在底面ABC内的射影为直线AC,∠A1AC为侧棱AA1与底面ABC所成的角,由此能求出侧棱A1A与底面ABC所成角的大小.(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1 , 由已知得∠A1NM即为所求二面角的平面角,由此能求出侧面A1ABB1与底面ABC所成二面角的大小.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则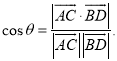 .
.


科目:初中数学 来源: 题型:
【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 
(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X) 附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若对任意的实数a,函数f(x)=(x﹣1)lnx﹣ax+a+b有两个不同的零点,则实数b的取值范围是( )
A.(﹣∞,﹣1]
B.(﹣∞,0)
C.(0,1)
D.(0,+∞)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在极坐标系中,点 ![]() ,曲线
,曲线 ![]() .以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
.以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
(Ⅱ)设点M为曲线C上的动点,求|MA|2+|MB|2取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边长分别为a、b、c.设S为△ABC的面积,满足S= ![]() (a2+c2﹣b2). (Ⅰ)求B;
(a2+c2﹣b2). (Ⅰ)求B;
(Ⅱ)若b= ![]() ,求(
,求( ![]() ﹣1)a+2c的最大值.
﹣1)a+2c的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在关于x的分式方程 ![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均为实数,方程①的根为非负数.
(1)求k的取值范围;
(2)当方程②有两个整数根x1、x2 , k为整数,且k=m+2,n=1时,求方程②的整数根;
(3)当方程②有两个实数根x1、x2 , 满足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k为负整数时,试判断|m|≤2是否成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com