
【题目】已知椭圆C: ![]() =1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
=1(a>0)的焦点在x轴上,且椭圆C的焦距为2. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.
【答案】解:(Ⅰ)∵椭圆 ![]() 的焦点在x轴上, ∴a2>7﹣a2 , 即
的焦点在x轴上, ∴a2>7﹣a2 , 即 ![]() ,
,
∵椭圆C的焦距为2,且a2﹣b2=c2 ,
∴a2﹣(7﹣a2)=1,解得a2=4,
∴椭圆C的标准方程为 ![]() ;
;
(Ⅱ)证明:由题知直线l的斜率存在,
设l的方程为y=k(x﹣4),点P(x1 , y1),Q(x2 , y2),N(x1 , ﹣y1),
则 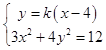 得3x2+4k2(x﹣4)2=12,
得3x2+4k2(x﹣4)2=12,
即(3+4k2)x2﹣32k2x+64k2﹣12=0,△>0, ![]() ,
, ![]() ,
,
由题可得直线QN方程为 ![]() ,
,
又∵y1=k(x1﹣4),y2=k(x2﹣4),
∴直线QN方程为 ![]() ,
,
令y=0,整理得 ![]() =
= ![]()
=  =
= 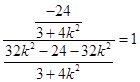 ,
,
即直线QN过点(1,0),
又∵椭圆C的右焦点坐标为F(1,0),
∴三点N,F,Q在同一条直线上.
【解析】(Ⅰ)由椭圆的焦点位置分析可得a2>7﹣a2 , 进而由椭圆的几何性质可得a2﹣(7﹣a2)=1,解可得a的值,代入椭圆的方程即可得答案;(Ⅱ)分析可得直线l的斜率存在,设l的方程为y=k(x﹣4),联立直线与椭圆的方程,由根与系数的关系分析可得直线QN方程,令y=0,可得直线QN过点(1,0),由椭圆的几何性质分析可得答案.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】嘉兴教育学院大学生小王利用暑假开展了30天的社会实践活动,参与了嘉兴浙北超市的经营,了解到某成本为15元/件的商品在x天销售的相关信息,如表表示:
销售量p(件) | P=45﹣x |
销售单价q(元/件) | 当1≤x≤18时,q=20+x |
设该超市在第x天销售这种商品获得的利润为y元.
(1)求y关于x的函数关系式;
(2)在这30天中,该超市销售这种商品第几天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED. 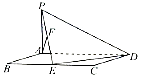
(1)求证:PA⊥平面ABCD;
(2)求直线BF与平面AFD所成角的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设F为抛物线y2=4x的焦点,A,B,C为该抛物线上不同的三点, ![]() +
+ ![]() +
+ ![]() =
= ![]() ,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
A.2
B.3
C.6
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 ![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 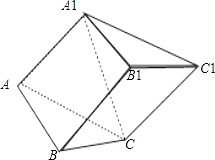
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,2b= ![]() asinB+bcosA,c=4. (Ⅰ)求A;
asinB+bcosA,c=4. (Ⅰ)求A;
(Ⅱ)若D是BC的中点,AD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移 ![]() 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲队修路500米与乙队修路800米所用天数相同,乙队比甲队每天多修30米,问甲队每天修路多少米?
解:设甲队每天修路x米,用含x的代表式完成表格:
甲队每天修路长度(单位:米) | 乙队每天修路长度(单位:米) | 甲队修500米所用天数(单位:天) | 乙队修800米所用天数(单位:天) |
x |
|
关系式:甲队修500米所用天数=乙队修800米所用天数
根据关系式列方程为:
解得:
检验:
答: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com