Question

【题目】如图，平行四边形ABCD中，BC=2AB=4，∠ABC=60°，PA⊥AD，E，F分别为BC，PE的中点，AF⊥平面PED．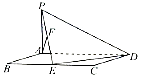
（1）求证：PA⊥平面ABCD；
（2）求直线BF与平面AFD所成角的正弦值．

Answer 1

【答案】
（1）解：连接AE，

∵AF⊥平面PED，ED平面PED，

∴AF⊥ED，

在平行四边形ABCD中，BC=2AB=4，∠ABC=60°，

∴AE=2， ，

∴AE2+ED2=AD2，∴AE⊥ED，

又∵AF∩AE=A，AF平面PAE，PA平面PAE，

∴ED⊥平面PAE，∵PA平面PAE，

∴ED⊥PA，

又PA⊥AD，AD∩ED=D，AE平面ABCD，AD平面ABCD，

∴PA⊥平面ABCD

（2）解：以E为坐标原点，以EA，ED为x轴，y轴建立如图所示的空间直角坐标系，

则A（0，2，0）， ， ，

∵AF⊥平面PED，所以AF⊥PE，

又F为PE中点，∴PA=AE=2，

∴P（0，2，2），F（0，1，1），

∴ ， ， ，

设平面AFD的法向量为 ，

由 ， 得， ，

令x=1，得 ．

设直线BF与平面AFD所成的角为θ，则： ，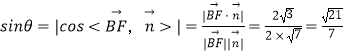

即直线BF与平面AFD所成角的正弦值为 ．

【解析】（1）利用勾股定理的逆定理得出AE⊥DE，由AF⊥平面PED得DE⊥AF，故而DE⊥平面PAE，于是DE⊥PA，结合PA⊥AD得出PA⊥平面ABCD；（2）以E为原点建立空间坐标系，求出平面ADF的法向量 ，则|cos＜ ＞|为直线BF与平面AFD所成角的正弦值．