
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=2x+4�ֱ�x�ᣬy���ڵ�A��C����D��m��2����ֱ��AC�ϣ���B��x���������ϣ���OB=3OC����E��y��������һ��ǵ�EΪ��0��n����
��1�����D�����꼰ֱ��BC�Ľ���ʽ��
��2������DE�����߶�DE�Ƶ�D��˳ʱ����ת90����߶�DG����������DEFG���Ƿ����n��ֵ��ʹ�����εĶ���F���ڡ�ABC�ı��ϣ������ڣ������������������n��ֵ���������ڣ�˵�����ɣ�
��3������E����AC�ĶԳƵ�E������nΪ��ֵʱ��A E���ֱ���AC��BC��AB��ֱ��
���𰸡�
��1��
�⣺��ֱ��y=2x+4��
��x=0ʱ��y=4����C��0,4����
��y=0ʱ��x=-2,��A��-2,0����
��D��m,2����ֱ��y=2x+4�ϣ���2x+4=2����D��-1,2����
��C��0��4����OB=3OC��
��OB=3��4=12��
��B��12,0��.
��BC�Ľ���ʽΪy=kx+b��
��![]()
���![]()
��ֱ��BC�Ľ���ʽΪy=![]() x+4.
x+4.
��2��
�⣺����D��y��Ĵ���DM��y���ڵ�M������F��y��Ĵ���FN��y���ڵ�N��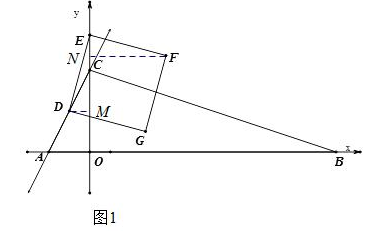
���DME=��FNE=90�㣬��DEM+��EDM=90�㣬
��������DEFG��
��DE=EF����DEF=90�㣬
���DEM+��FEN=90�㣬
���EDM=��FEN��
���DME�ա�ENF,
��FN=EM=|n-2|��EN=DM=1��
��ON=OE-EN=|n-1|��
��F��|n-2|��|n-1|��
����F��BC��ʱ��F��n-2,n-1������������ֱ��BC�Ľ���ʽy=![]() x+4��
x+4��
��![]() (n-2)+4=n-1�����n=
(n-2)+4=n-1�����n=![]() ��
��
����F��AB��ʱ����n-1=0����n=1��
����n=![]() ��1.
��1.
��3��
�⣺�ٵ�AE����ACʱ��A��E��E'���㹲�ߣ���ͼ2����AE��AC��

��֤�á�ACE~��OCA��
��![]()
��AC=![]() =
=![]() =2
=2![]() .
.
��CE=![]() =5��
=5��
��n=4-5=-1.
�ڵ�AE����ABʱ����EE'��AC�Ľ���ΪP����ͼ3���ɵá�AE'P�ա�CEP��

��AE=AE'=CE=4-n��
��Rt��AEO����AE2=AO2+OE2��
����4-n��2=22+n2��
���n=![]()

����ͼ3����AE'��BC��ֱʱ��ֱ��AE����BC���ӳ��߽��ڵ�M����y�ύ�ڵ�Q��
��tan��OAQ=tan��MCQ=tan��BCO=![]() =3��
=3��
����OQ=3OA=6����Q��0,6����
��A��-2,0����Q��0,6����ֱ��AQ�Ľ���ʽΪy=3x+6.
��Ϊֱ��AC�Ľ���ʽΪy=2x+4��AC��EE'��ֱ��
���Կ���EE'�Ľ���ʽΪy=-![]() x+c��
x+c��
��E��0��n������ɽ��y=-![]() x+n.
x+n.
����![]()
���![]()
��E'��![]() ,
,![]() )��
)��
��EE'���е�P������Ϊ��![]() ��
��![]() ����
����
��Ϊ��P��ֱ��AC�ϣ�����y=2x+4�ɵ�
![]() +4=
+4=![]() ��
��
���n=![]() .
.
����n=-1��![]() ��
��![]() .
.
��
�⣺�ٵ�AE����ACʱ��A��E��E'���㹲�ߣ���ͼ2����AE��AC��

��֤�á�ACE~��OCA��
��![]()
��AC=![]() =
=![]() =2
=2![]() .
.
��CE=![]() =5��
=5��
��n=4-5=-1.
�ڵ�AE����ABʱ����EE'��AC�Ľ���ΪP����ͼ3���ɵá�AE'P�ա�CEP��

��AE=AE'=CE=4-n��
��Rt��AEO����AE2=AO2+OE2��
����4-n��2=22+n2��
���n=![]()

����ͼ3����AE'��BC��ֱʱ��ֱ��AE����BC���ӳ��߽��ڵ�M����y�ύ�ڵ�Q��
��tan��OAQ=tan��MCQ=tan��BCO=![]() =3��
=3��
����OQ=3OA=6����Q��0,6����
��A��-2,0����Q��0,6����ֱ��AQ�Ľ���ʽΪy=3x+6.
��Ϊֱ��AC�Ľ���ʽΪy=2x+4��AC��EE'��ֱ��
���Կ���EE'�Ľ���ʽΪy=-![]() x+c��
x+c��
��E��0��n������ɽ��y=-![]() x+n.
x+n.
����![]()
���![]()
��E'��![]() ,
,![]() )��
)��
��EE'���е�P������Ϊ��![]() ��
��![]() ����
����
��Ϊ��P��ֱ��AC�ϣ�����y=2x+4�ɵ�
![]() +4=
+4=![]() ��
��
���n=![]() .
.
����n=-1��![]() ��
��![]() .
.
��
�⣺�ٵ�AE����ACʱ��A��E��E'���㹲�ߣ���ͼ2����AE��AC��

��֤�á�ACE~��OCA��
��![]()
��AC=![]() =
=![]() =2
=2![]() .
.
��CE=![]() =5��
=5��
��n=4-5=-1.
�ڵ�AE����ABʱ����EE'��AC�Ľ���ΪP����ͼ3���ɵá�AE'P�ա�CEP��

��AE=AE'=CE=4-n��
��Rt��AEO����AE2=AO2+OE2��
����4-n��2=22+n2��
���n=![]()

����ͼ3����AE'��BC��ֱʱ��ֱ��AE����BC���ӳ��߽��ڵ�M����y�ύ�ڵ�Q��
��tan��OAQ=tan��MCQ=tan��BCO=![]() =3��
=3��
����OQ=3OA=6����Q��0,6����
��A��-2,0����Q��0,6����ֱ��AQ�Ľ���ʽΪy=3x+6.
��Ϊֱ��AC�Ľ���ʽΪy=2x+4��AC��EE'��ֱ��
���Կ���EE'�Ľ���ʽΪy=-![]() x+c��
x+c��
��E��0��n������ɽ��y=-![]() x+n.
x+n.
����![]()
���![]()
��E'��![]() ,
,![]() )��
)��
��EE'���е�P������Ϊ��![]() ��
��![]() ����
����
��Ϊ��P��ֱ��AC�ϣ�����y=2x+4�ɵ�
![]() +4=
+4=![]() ��
��
���n=![]() .
.
����n=-1��![]() ��
��![]() .
.
����������1������D��m,2������ֱ��AC�Ľ���ʽ�����m����ֱ��AC�Ľ���ʽ�ɵõ�C�����꣬��OB=3OC�������B�����꣬���ô���ϵ������BC�Ľ���ʽ��
��2���������ε����ʹ���ȫ�������Σ���n��ʾ����F�����꣬�ٷ������۵�F��BC�Ϻ���AB��ʱn��ֵ��
��3��������������ۣ�EE'��AC��EE'��AB��EE'��BC.


 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=90�㣬AD��BC������ΪD��������ABC��ƽ���ߣ��ֱ�AD��AD��P��Q���㣻��֤��AP=AQ����Ҫ�߹���ͼ��������ͼ�ۼ�����д������ 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABE�С�A=90�㣬��B=60�㣬BE=10��D���߶�AE�ϵ�һ���㣬��D��CD��BE��C����ʹ�á�CDE=30�㣬��CD���ȵ�ȡֵ��Χ�� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˽���ѧԺ��ѧ��С��������ٿ�չ��30������ʵ����������˼����㱱���еľ�Ӫ���˽ij�ɱ�Ϊ15Ԫ/������Ʒ��x�����۵������Ϣ�������ʾ��
������p������ | P=45��x |
���۵���q��Ԫ/���� | ��1��x��18ʱ��q=20+x |
��ó����ڵ�x������������Ʒ��õ�����ΪyԪ��
��1����y����x�ĺ�����ϵʽ��
��2������30���У��ó�������������Ʒ�ڼ�������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ����ij����Һ����ʾ���IJ���ͼ����ʾ��AO�����Ƶ�O��תһ���ĽǶȣ��о���������ʾ������A�����B������AB��ˮƽ��BC��ֱʱ����ͼ�ڣ����˹ۿ���Ļ�����ʣ���ʱ��á�BAO��15�㣬AO��30cm����OBC��45�㣬��AB�ij��ȣ��������ȷ��1 cm�����ο����ݣ�sin15���0.26��cos15���0.97�� tan15���0.27�� ![]() ��1.414��
��1.414��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪P��������y2=4x�ϵĶ��㣬Q��ԲC����x+3��2+��y��3��2=1�ϣ�R��P��y���ϵ���Ӱ����|PQ|+|PR|����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���費��ʽ0��|x+2|��|1��x|��2�Ľ⼯ΪM��a��b��M
��1��֤����|a+ ![]() b|��
b|�� ![]() ��
��
��2���Ƚ�|4ab��1|��2|b��a|�Ĵ�С����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�BC=2AB=4����ABC=60�㣬PA��AD��E��F�ֱ�ΪBC��PE���е㣬AF��ƽ��PED�� 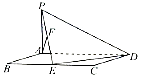
��1����֤��PA��ƽ��ABCD��
��2����ֱ��BF��ƽ��AFD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC�����ڽ�A��B��C�ĶԱߣ�2b= ![]() asinB+bcosA��c=4�� ������A��
asinB+bcosA��c=4�� ������A��
������D��BC���е㣬AD= ![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com