
【题目】在极坐标系中,点 ![]() ,曲线
,曲线 ![]() .以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
.以极点为坐标原点,极轴为x轴正半轴建立平面直角坐标系. (Ⅰ)在直角坐标系中,求点A,B的直角坐标及曲线C的参数方程;
(Ⅱ)设点M为曲线C上的动点,求|MA|2+|MB|2取值范围.
【答案】解:(I)利用 ![]() ,则点
,则点 ![]() 的直角坐标分别为:A
的直角坐标分别为:A 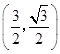 ,B
,B ![]() . 曲线
. 曲线 ![]() .即ρ2=2ρ
.即ρ2=2ρ 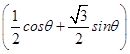 ,化为直角坐标方程:x2+y2﹣x﹣
,化为直角坐标方程:x2+y2﹣x﹣ ![]() y=0.
y=0.
配方为: ![]() +
+ ![]() =1.
=1.
可得参数方程为: 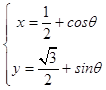 .
.
(II)不妨设M  ,
,
则|MA|2+|MB|2=(cosα﹣1)2+sin2θ+ ![]() +
+ ![]() =4﹣cosα﹣
=4﹣cosα﹣ ![]() sinα=4﹣2sin
sinα=4﹣2sin ![]() .
.
∵sin ![]() ∈[﹣1,1],则4﹣2sin
∈[﹣1,1],则4﹣2sin ![]() ∈[2,6].
∈[2,6].
因此:|MA|2+|MB|2取值范围是[2,6]
【解析】(I)利用 ![]() ,可得A,B直角坐标.曲线
,可得A,B直角坐标.曲线 ![]() .即ρ2=2ρ
.即ρ2=2ρ ![]() ,即可化为直角坐标方程,通过配方利用平方关系可得参数方程.(II)不妨设M
,即可化为直角坐标方程,通过配方利用平方关系可得参数方程.(II)不妨设M ![]() ,可得|MA|2+|MB|2=4﹣2sin
,可得|MA|2+|MB|2=4﹣2sin ![]() .利用sin
.利用sin ![]() ∈[﹣1,1],即可得出.
∈[﹣1,1],即可得出.


科目:初中数学 来源: 题型:
【题目】设F为抛物线y2=4x的焦点,A,B,C为该抛物线上不同的三点, ![]() +
+ ![]() +
+ ![]() =
= ![]() ,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
,O为坐标原点,且△OFA、△OFB、△OFC的面积分别为S1、S2、S3 , 则S12+S22+S32=( )
A.2
B.3
C.6
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知斜三棱柱ABC﹣A1B1C1 的侧面 A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2 ![]() ,且AA1⊥A1C,AA1=A1C.
,且AA1⊥A1C,AA1=A1C. 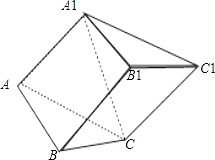
(1)求侧棱A1A与底面ABC所成角的大小;
(2)求侧面A1ABB1与底面ABC所成二面角的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,2b= ![]() asinB+bcosA,c=4. (Ⅰ)求A;
asinB+bcosA,c=4. (Ⅰ)求A;
(Ⅱ)若D是BC的中点,AD= ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ![]() ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
,DC=SD=2,点M在侧棱SC上,∠ABM=60°. 
(Ⅰ)证明:M是侧棱SC的中点;
(Ⅱ)求二面角S﹣AM﹣B的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(φ>0,﹣π<φ<0)的最小正周期是π,将f(x)图象向左平移 ![]() 个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
个单位长度后,所得的函数图象过点P(0,1),则函数f(x)( )
A.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
B.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
C.在区间[﹣ ![]() ,
, ![]() ]上单调递减
]上单调递减
D.在区间[﹣ ![]() ,
, ![]() ]上单调递增
]上单调递增
查看答案和解析>>
科目:初中数学 来源: 题型:
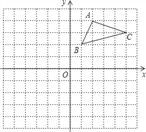
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】足球比赛规定:胜一场得3分,平一场得1分,负一场得0分.某足球队共进行了6场比赛,得了12分,该队获胜的场数可能是( )
A.1或2
B.2或3
C.3或4
D.4或5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com