
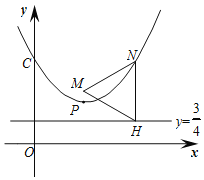
【题目】如图,抛物线的顶点P(m,1)(m>0),与y轴的交点C(0,m2+1).
(1)求抛物线的解析式(用含m的式子表示)
(2)点N(x,y)在该抛物线上,NH⊥直线y=![]() 于点H,点M(m,
于点H,点M(m,![]() )且∠NMH=60°.
)且∠NMH=60°.
①求证:△MNH是等边三角形;
②当点O、P、N在同一直线上时,求m的值.
【答案】(1)该抛物线解析式是:y=(x﹣m)2+1;(2)①证明见解析;②联立方程组,解得m=![]() .
.
【解析】
(1)设抛物线解析式把点C的坐标代入即可求得a的值;
(2)①证明NM=NH即可;
②求点M、N的纵坐标的数量关系,得到点N的纵坐标;再求直线OP的解析式,求m的值.
解:(1)设抛物线解析式是y=a(x﹣m)2+1(a≠0),
将C(0,m2+1)代入,得a(0﹣m)2+1=m2+1
解得a=1.
故该抛物线解析式是:y=(x﹣m)2+1;
(2)①根据题意知,NH=y﹣![]() .
.
NM=![]() =
=![]() =
=![]() =y﹣
=y﹣![]() .
.
则NM=NH.
又因为∠NMH=60°,
所以△MNH是等边三角形;
②由①知,△MNH是等边三角形.则yM=![]() yN,即
yN,即![]() =
=![]() y.故yN=
y.故yN=![]() .
.
由于点N(x,![]() )在抛物线y=(x﹣m)2+1上,
)在抛物线y=(x﹣m)2+1上,
∴(x﹣m)2+1=![]() ①
①
所以点N的坐标是(x,(x﹣m)2+1).
设直线OP的解析式是y=kx(k≠0).
把P(m,1)(m>0)代入,得mk=1.
解得k=![]() .
.
故该直线方程是y=![]() .
.
把N(x,(x﹣m)2+1)代入,得(x﹣m)2+1=![]() ②.
②.
②联立方程组,解得m=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC是一块锐角三角形余料,边BC=120 mm,高AD=80mm,要把它加工成矩形零件PQMN,使矩形PQMN的边QM在BC上,其余两个项点P,N分别在AB,AC上.
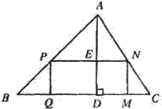
(1)当矩形的边PN=PQ时,求此时矩形零件PQMN的面积;
(2)求这个矩形零件PQMN面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
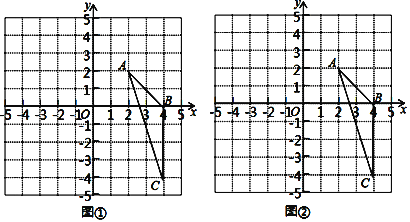
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)将△ABC绕点A顺时针旋转90°后得到△AB1C1,在图①中画出△AB1C1,并求出在旋转过程中△ABC扫过的面积;
(2)在图②中以点O为位似中心,将△ABC缩小为原来的![]() ,并写出点C的对应点的坐标.
,并写出点C的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.
(1)写出y与x中间的函数关系式和自变量![]() 的取值范围;
的取值范围;
(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,O是AC的中点,把Rt△ABC绕着点O旋转得到Rt△A'B'C',使得点C的对应点C'恰好落在AB上,则C,C'两点间的距离是_____.
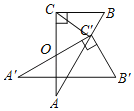
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,地物线点![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 均不为0)的顶点为
均不为0)的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,我们称以
,我们称以![]() 为顶点,对称轴是
为顶点,对称轴是![]() 轴且过点
轴且过点![]() 的抛物线为抛物线
的抛物线为抛物线![]() 的衍生抛物线,直线
的衍生抛物线,直线![]() 为抛物线
为抛物线![]() 的衍生直线.
的衍生直线.
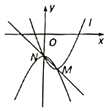
(1)求抛物线![]() 的衍生抛物线和衍生直线的解析式;
的衍生抛物线和衍生直线的解析式;
(2)若一条抛物线的衍生抛物线和衍生直线分别是![]() 和
和![]() ,求这条抛物线的解析式.
,求这条抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
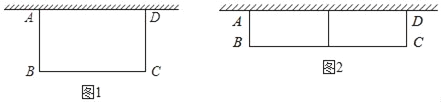
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O 为坐标原点,P是反比例函数![]() 图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
图象上任意一点,以P为圆心,PO为半径的圆与x轴交于点 A、与y轴交于点B,连接AB.
(1)求证:P为线段AB的中点;
(2)求△AOB的面积.
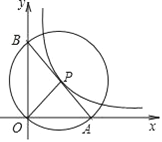
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在将式子![]() (m>0)化简时,
(m>0)化简时,
小明的方法是:![]() =
=![]() =
=![]() =
=![]() ;
;
小亮的方法是: ![]() ;
;
小丽的方法是:![]() .
.
则下列说法正确的是( )
A. 小明、小亮的方法正确,小丽的方法不正确
B. 小明、小丽的方法正确,小亮的方法不正确
C. 小明、小亮、小丽的方法都正确
D. 小明、小丽、小亮的方法都不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com