

 或
或 .
.
 ,
, ,
,  .
.

 ,
, ,
,  .
. ,
, 时,对称轴为t=
时,对称轴为t= ,
,
 ,
,


 ,
,

 或
或 时,△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形.
时,△APQ绕它的一边中点旋转180°,旋转前后两个三角形组成的四边形为矩形.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源:不详 题型:解答题
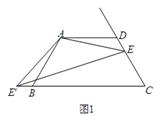
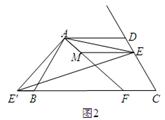
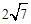 ,求ME的长.
,求ME的长. 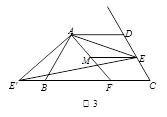
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
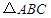 绕点
绕点 按逆时针方向旋转,旋转角为
按逆时针方向旋转,旋转角为 ,旋转后使各边长变为原来的
,旋转后使各边长变为原来的 倍,得到
倍,得到 ,我们将这种变换记为[
,我们将这种变换记为[ ].
].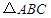 作变换[
作变换[ ]得
]得 ,则
,则 :
: = ___;直线
= ___;直线 与直线
与直线 所夹的锐角为 __ °;
所夹的锐角为 __ °;
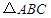 中,
中,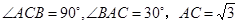 ,对
,对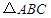 作变换[
作变换[ ]得
]得 ,使得四边形
,使得四边形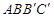 为梯形,其中
为梯形,其中 ∥
∥ ,且梯形
,且梯形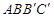 的面积为
的面积为 ,求
,求 和
和 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
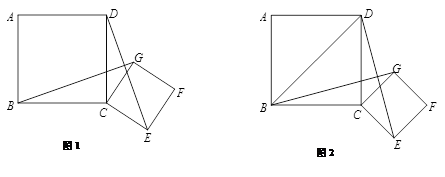
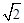 ,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.
,将正方形CEFG绕着点C旋转到某一位置时恰好使得CG//BD,BG=BD.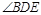 的度数;
的度数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com