
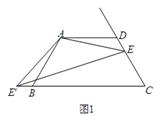
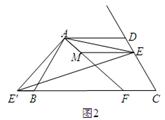
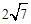 ,求ME的长.
,求ME的长. 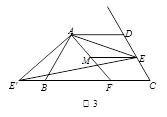
 ;
; 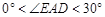 时,
时,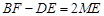 ;
;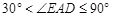 时,
时, ;
; 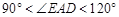 时,
时, ;
;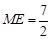 .
. E'N,EN=
E'N,EN= NE',再ME∥BC,得到
NE',再ME∥BC,得到 ,从而得到线段DE、BF、ME之间的数量关系;
,从而得到线段DE、BF、ME之间的数量关系;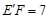 ,再由(2)的结论得到ME的长.
,再由(2)的结论得到ME的长. E'N,
E'N, NE',
NE', ,而E'B=DE,
,而E'B=DE, ;
; 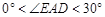 时,
时,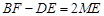 ;
;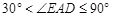 时,
时, ;
; 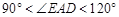 时,
时, ;
;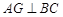 于点G, 作
于点G, 作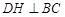 于点H.
于点H.
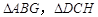 .
. ,
, 、B、C在一条直线上.
、B、C在一条直线上.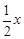 ,.
,.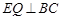 于Q.
于Q.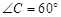 ,
,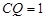 ,
, 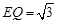 .
.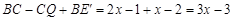 .
. 于点P.
于点P. 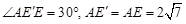 .
.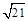 .
. .
. 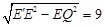 .
. 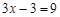 .
.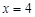 .
.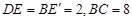 ,
,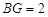 .
.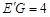
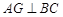 ,
,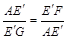
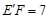 .
.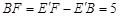 .
.
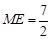 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+ ;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
;…按此规律继续旋转,直到点P2012为止,则AP2012等于( )
A.2 011+671 | B.2 012+671 |
C.2 013+671 | D.2 014+671 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.60 ° | B.75° | C.85° | D.90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com