Question

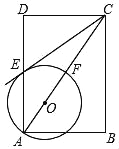
【题目】如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD，AC分别交于点E，F，且∠ACB＝∠DCE．

（1）求证：CE是圆O所在圆的切线；

（2）若tan∠BAC＝，BC＝2，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；（2）r＝

【解析】

（1）连接OE．欲证直线CE与相切，只需证明∠CEO=90°，即OE⊥CE即可；
（2）在直角三角形ABC中，根据三角函数的定义可以求得 然后根据勾股定理求得 同理知DE=1；在Rt△COE中，利用勾股定理可以求得CO2=OE2+CE2，即从而易得r的值；

（1）证明：∵四边形ABCD是矩形，

∴BC∥AD，∠BCA＝∠DAC；

又∵∠ACB＝∠DCE，

∴∠DAC＝∠DCE；

连接OE，则∠DAC＝∠AEO＝∠DCE；

∵∠DCE+∠DEC＝90°，

∴∠AEO+∠DEC＝90°，

∴∠OEC＝90°，即OE⊥CE，

又OE是⊙O的半径，

∴直线CE与⊙O相切；

（2）∵

∴

∴

∵∠DCE=∠ACB,

∴

∴DE＝DCtan∠DCE＝1；

在Rt△CDE中，

设⊙O的半径为r，则在Rt△COE中，CO2＝OE2+CE2，

即

解得：