【题目】电动自行车已成为市民日常出行的首选工具。据某市品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月销售216辆.
（1）求该品牌电动车销售量的月平均增长率；
（2）若该品牌电动自行车的进价为2300元，售价2800元，则该经销商1月至3月共盈利多少元？
【答案】（1）20％；（2）273000.
【解析】
试题（1）设该品牌电动车销售量的月平均增长率为x，2月份该品牌电动车销售量为150(1＋x)，则3月份该品牌电动车销售量为150(1＋x) (1＋x) ＝150(1＋x)2. 据此列出方程求解.
（2）根据（1）求出增长率后，再计算出二月份的销量，即可得到答案．
试题解析：解：（1）设该品牌电动车销售量的月平均增长率为x，根据题意得
150（1+x）2=216，
解得x1=0.2，x2=-2.2（舍去）.
答：该品牌电动车销售量的月平均增长率为20％.
（2）由（1）得该品牌电动车销售量的月平均增长率为20％，
∴2月份的销售量为150×（1+20％）=180.
∴则1-3月份的销售总量为150+180+216=546（辆）
∴
（元）
答：该经销商1月至3月共盈利273000元.
科目：初中数学 来源： 题型：
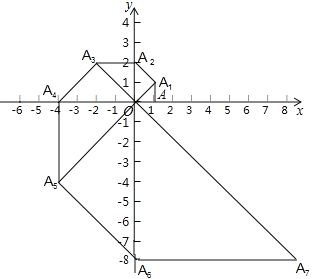
【题目】如图，在平面直角坐标系中，等腰直角三角形OAA1的直角边OA在x轴上，点A1在第一象限，且OA＝1，以点A1为直角顶点，0A1为一直角边作等腰直角三角形OA1A2，再以点A2为直角顶点，OA2为直角边作等腰直角三角形OA2A3…依此规律，则点A2019的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】由于检修部分生产设备，生产能力下降，某工厂现在比原计划平均每天少生产30台机器，现在生产600台机器所需时间与原计划生产900台机器所需时间相同.
问现在平均每天生产多少台机器.
（1）设现在平均每天生产
台机器，则用含的式子表示；
原计划平均每天生产______台机器，现在生产600台机器所需时间为______天，原计划生产900台机器所需时间为______天；
（2）列出方程，完成本题解答.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知命题：①两边和第三边上的中线对应相等的两个三角形全等；②腰长和面积对应相等的两个等腰三角形全等，则下列判断正确的是（ ）
A.①，②都是真命题B.①是真命题，②是假命题
C.①是假命题，②是真命题D.①，②都是假命题
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠BAC=90°，BC=10，tan∠ABC=
，点O是AB边上的动点，以O为圆心，OB为半径的⊙O与边BC的另一交点为D，过点D作AB的垂线，交于点E，连结BE、AE．
（1）当AE∥BC（如图（1））时，求⊙O的半径；
（2）设BO=x，AE=y，求y关于x的函数关系式；
（3）若以A为圆心的⊙A与⊙O有公共点D、E，当恰好也过点C时，求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】列方程解应用题：
云阳县多集合生态农业有限公司在2018年种植玉米的平均亩产量为0. 75吨，该公司总结了种植玉米的经验，2019年该公司种植玉米的情况是：种植面积比2018年减少了10%、平均亩产量比2018年增加了0. 2吨，总产量比2018年增加了8. 4吨.
（1）求2018年该公司种植玉米的面积；
（2）若2019年该公司种植玉米的人数比2018年少了12人，人均种植面积比2018年增加了17%，求2019年该公司种植玉米的人数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为奖励优秀学生，某校准备购买一批文具袋和圆规作为奖品，已知购买1个文具袋和2个圆规需21元，购买2个文具袋和3个圆规需39元。
（1）求文具袋和圆规的单价。
（2）学校准备购买文具袋20个，圆规若干，文具店给出两种优惠方案：
方案一：购买一个文具袋还送1个圆规。
方案二：购买圆规10个以上时，超出10个的部分按原价的八折优惠，文具袋不打折.
①设购买面规m个，则选择方案一的总费用为______，选择方案二的总费用为______.
②若学校购买圆规100个，则选择哪种方案更合算？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.
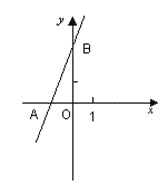
（1）求A，B两点的坐标；
（2）过B点作直线BP与x轴相交于P，且使OP=2OA， 求ΔABP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
