
����Ŀ��Ϊ��������ѧ����ijУ������һ���ľߴ���Բ����Ϊ��Ʒ����֪����1���ľߴ���2��Բ����21Ԫ������2���ľߴ���3��Բ����39Ԫ��
��1�����ľߴ���Բ��ĵ��ۡ�
��2��ѧУ�������ľߴ�20����Բ�����ɣ��ľߵ���������Żݷ�����
����һ������һ���ľߴ�����1��Բ�档
������������Բ��10������ʱ������10���IJ��ְ�ԭ�۵İ����Żݣ��ľߴ�������.
���蹺�����m������ѡ��һ���ܷ���Ϊ______��ѡ�������ܷ���Ϊ______.
����ѧУ����Բ��100������ѡ�����ַ��������㣿��˵������.
���𰸡���1���ľߴ��ĵ���Ϊ15Ԫ��Բ�浥��Ϊ3Ԫ;��2���ٷ���һ�ܷ���Ϊ![]() Ԫ,
Ԫ,
�������ܷ���Ϊ![]() Ԫ���ڷ���һ������.
Ԫ���ڷ���һ������.
��������
��1�����ľߴ��ĵ���ΪxԪ/����Բ��ĵ���ΪyԪ/��������������1���ľߴ���2��Բ����21Ԫ������2���ľߴ���3��Բ����39Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2�������ܼ�=������������������Żݷ������蹺�����m�����ֱ����ѡ��һ��ѡ����������ã�Ȼ�����m=100����ȽϺɵó����ۣ�
��1�����ľߴ��ĵ���ΪxԪ��Բ�浥��ΪyԪ��
�������![]() ���
���![]()
���ľߴ��ĵ���Ϊ15Ԫ��Բ�浥��Ϊ3Ԫ��
��2������Բ��m������һ�ܷ���Ϊ��![]() Ԫ
Ԫ
�������ܷ���![]() Ԫ
Ԫ
�ʴ�Ϊ��![]() Ԫ��
Ԫ��![]()
����Բ��100��ʱ������һ�ܷ��ã�![]() Ԫ��
Ԫ��
�������ܷ��ã�![]() Ԫ��
Ԫ��
������һ�����㡣



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����С��Ϊ�˽�ͬѧ�Ƕ�ѧУ�������ܲ������ϲ���̶�,��ȡ����ѧ�����е���.�������ÿ��ѧ����A(�dz�ϲ��)��B(�Ƚ�ϲ��)��C(һ��)��D(��ϲ��)�ĸ��ȼ��Ի����.ͼ1��ͼ2�Ǹ�С��ɼ����ݺ���Ƶ�����ͳ��ͼ.��ȷ������ͳ��ͼ����ȷ�ģ�������ͳ��ͼ����һ�������Ҳ�������.�������ͳ��ͼ�ṩ����Ϣ������������⣺

(1)�˴ε����ѧ������Ϊ___��
(2)����ͳ��ͼ�д��ڴ������___(��A. B.C�е�һ��)������ͼ�м��Ը�����
(3)��ͼ2�в�������ͳ��ͼ�в������IJ��֣�
(4)�����У��600��ѧ������ô�Դ˻���dz�ϲ���������Ƚ�ϲ������ѧ�����ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����ƽ��ֱ������ϵ������OAB�Ķ�������ֱ�ΪO��0��0����A��2��1����B��1��-2����
��1����ԭ��OΪλ����������y����Ҳ����OAB��һ��λ�ơ�OA1B1 ��ʹ�����OAB�����Ʊ�Ϊ2��1�����ֱ�д����A��B�Ķ�Ӧ��A1��B1��������
��2����������OAB����ƽ��2����λ��������ƽ��1����λ�����O2A2B2 ����д����A��B�Ķ�Ӧ��A2��B2��������
��3���жϡ�OA1B1���O2A2B2 ���ܷ��ǹ���ijһ��MΪλ�����ĵ�λ��ͼ��������������ͼ�б��λ������M����д����M��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
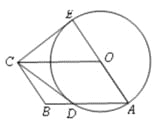
����Ŀ����ͼ���ı���OABC��ƽ���ı��Σ���OΪԲ�ģ�OAΪ�뾶��Բ��AB��D���ӳ� AO����O��E������CD��CE����CE����O�����ߣ�����������⣺
��1����֤��CD����O�����ߣ�
��2����ƽ���ı���OABC�����߳��Ƿ���![]() ����������ƽ���ı���OABC�����.
����������ƽ���ı���OABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����E��F�ֱ���ֱ��AB��CD�ϣ���G��H����ֱ��֮�䣬�߶�EF��GH�ཻ�ڵ�O�����С�AEF+��CFE��180�㣬��AEF����1����2������ͼ����ȵĽǹ��У�������

A. 5��B. 6��C. 7��D. 8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У�E��AB��һ�㣬�߶�DE�����ζԽ���AC���ڵ�F����O��AC���е㣬EO���ӳ��߽���DC�ڵ�G
��1����֤����AED����FBC��
��2����֤���ı���DEBG��ƽ���ı��Σ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵΪ�˱���������������![]() ��
��![]() �����ͺŵ���ˮ�����豸��10̨������ͬʱ������ͬ�ɷֵ���ˮ��������
�����ͺŵ���ˮ�����豸��10̨������ͬʱ������ͬ�ɷֵ���ˮ��������![]() ��6̨��
��6̨��![]() ��4̨��112����
��4̨��112����![]() ��4̨��
��4̨��![]() ��6̨����108��Ԫ.
��6̨����108��Ԫ.
��1�����![]() �͡�
�͡�![]() ����ˮ�����豸�ĵ��ۣ�
����ˮ�����豸�ĵ��ۣ�
��2�����˽⣬һ̨![]() ���豸ÿ�¿ɴ�����ˮ220�֣�һ̨
���豸ÿ�¿ɴ�����ˮ220�֣�һ̨![]() ���豸ÿ�¿ɴ�����ˮ190�֣��������ҵ�ƻ��ò�����106��Ԫ���ʽ����������豸������ʹ�������豸ÿ�µ���ˮ������������2005�֣���ͨ������˵�����ַ����Ƿ����.
���豸ÿ�¿ɴ�����ˮ190�֣��������ҵ�ƻ��ò�����106��Ԫ���ʽ����������豸������ʹ�������豸ÿ�µ���ˮ������������2005�֣���ͨ������˵�����ַ����Ƿ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1����2��Ҫʹ��ABD����ACD�������������������һ���������ѡ���ǣ� ��

A.��ADB����ADCB.��B����CC.AB��ACD.DB��DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽����
(1)���֣���ƽ���ڣ���BC��a��AC��b������a��b��
����A���߶�BC��ʱ(��ͼ1)���߶�AB�ij�ȡ����Сֵ����СֵΪ�� ����
����A���߶�BC�ӳ�����ʱ(��ͼ2)���߶�AB�ij�ȡ�����ֵ�����ֵΪ�� ����
(2)Ӧ�ã���AΪ�߶�BC��һ���㣬��ͼ3���ֱ���AB��ACΪ�ߣ����ȱߡ�ABD�͵ȱߡ�ACE������CD��BE��
��֤����CD��BE��
����BC��3��AC��1�����߶�CD���ȵ����ֵΪ�� ����
(3)��չ����ͼ4����ƽ��ֱ������ϵ�У���A������Ϊ(2��0)����B������Ϊ(5��0)����PΪ��AB��һ���㣬��PA��2��PM��PB����BPM��90�㣮��ֱ��д���߶�AM�������ֵ����ʱ��P�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com