[题目]已知:如图.点E.F分别在直线AB.CD上.点G.H在两直线之间.线段EF与GH相交于点O.且有∠AEF+∠CFE＝180°.∠AEF﹣∠1＝∠2.则在图中相等的角共有( )A. 5对B. 6对C. 7对D. 8对题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】已知：如图，点E、F分别在直线AB、CD上，点G、H在两直线之间，线段EF与GH相交于点O，且有∠AEF+∠CFE＝180°，∠AEF﹣∠1＝∠2，则在图中相等的角共有（　　）

A. 5对B. 6对C. 7对D. 8对

【答案】D

【解析】

依据∠AEF+∠CFE＝180°，即可得到AB∥CD，依据平行线的性质以及对顶角的性质，即可得到图中相等的角．

解：∵∠AEF+∠CFE＝180°，

∴AB∥CD，

∴∠AEF＝∠DFE，∠CFE＝∠BEF，

∵∠AEF﹣∠1＝∠2，∠AEF﹣∠1＝∠AEG，

∴∠AEG＝∠2，

∴∠1＝∠EFH，∠BEG＝∠CFH，

∴GE∥FH，

∴∠G＝∠H，

又∵∠EOG＝∠FOH，∠EOH＝∠GOF，

∴图中相等的角共有8对，

故选：D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，在平面直角坐标系中，直线y=x+2与x轴交于点A，与y轴交于点C，抛物线y=x2+bx+c经过A、C两点，与x轴的另一交点为点B．

（1）求抛物线的函数表达式；

（2）点D为直线AC上方抛物线上一动点；

①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1， △BCE的面积为S2，求的最大值；

②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对任意一个三位数n，如果n满足各个数位上的数字互不相同，且都不为零，那么称这个数为“相异数”，将一个“相异数”n的各个数位上的数字之和记为F（n）．例如n=135时，F（135）=1+3+5=9．

（1）对于“相异数”n，若F（n）=6，请你写出一个n的值；

（2）若a，b都是“相异数”，其中a=100x+12，b=350+y（1≤x≤9，1≤y≤9，x，y都是正整数），规定：k＝，当F（a）+F（b）=18时，求k的最小值．

查看答案和解析>>

科目：初中数学 来源： 题型：

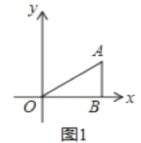
【题目】如图1,在平面直角坐标系中,点O为坐标原点,点A(3a,2a)在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,S△AOB=12，点M从O出发，沿y轴的正半轴以每秒2个单位长度的速度运动，点N从点B出发以每秒3个单位长度的速度向x轴负方向运动，点M与点N同时出发，设点M的运动时间为t秒，连接AM，AN，MN.

(1)求a的值；

(2)当0<t<2时，

①请探究∠ANM，∠OMN，∠BAN之间的数量关系，并说明理由；

②试判断四边形AMON的面积是否变化?若不变化，请求出其值；若变化，请说明理由。

(3)当OM=ON时，请求出t的值。