
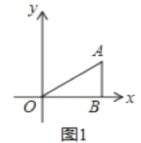
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,��OΪ����ԭ��,��A(3a,2a)�ڵ�һ����,����A��x��������,����Ϊ��B,����OA,S��AOB=12����M��O��������y�����������ÿ��2����λ���ȵ��ٶ��˶�����N�ӵ�B������ÿ��3����λ���ȵ��ٶ���x�Ḻ�����˶�����M���Nͬʱ���������M���˶�ʱ��Ϊt�룬����AM��AN��MN.
(1)��a��ֵ��
(2)��0<t<2ʱ��
����̽����ANM����OMN����BAN֮���������ϵ����˵�����ɣ�
�����ж��ı���AMON������Ƿ�仯?�����仯���������ֵ�����仯����˵�����ɡ�
(3)��OM=ONʱ�������t��ֵ��
���𰸡���1��a=2����2���١�ANM=��OMN+��BAN�����ɼ�����. ���ı���AMON��������䣬���ɼ�����. ��3��t=![]() ��6
��6
��������
1��������AOB������г����̼��ɽ�����⣻
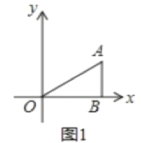
��2����0<t<2ʱ�١�ANM=��OMN+��BAN����ͼ2�У���N����NH��AB������ƽ�е�����֤�����ɣ��ڸ���S�ı���AMON=S�ı���ABOM-S��ABN�����㼴�ɣ�
��3����OM=ON���õ�2t=63t��2t=3t6�������.
(1)��ͼ1�У�
��S��AOB=12,A(3a,2a)��
��![]() ��3a��2a=12��
��3a��2a=12��
��a![]() =4��
=4��
�֡�a>0��
��a=2.
(2)��0<t<2ʱ
�١�ANM=��OMN+��BAN��ԭ�����£�
��ͼ2��,��N����NH��AB��
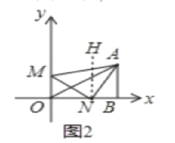
��AB��X��
��AB��OM
��AB��NH��OM
���OMN=��MNH
��BAN=��ANH
���ANM=��MNH+��ANH=��OMN+��BAN.
��S�ı���AMON=12���������£�
��a=2
��A(6,4)
��OB=6��AB=4��OM=2tBN=3t
ON=63t
��S�ı���AMON=S�ı���ABOMS��ABN,= ![]() (AB+OM)��OB
(AB+OM)��OB![]() ��BN��AB=
��BN��AB=![]() (4+2t)��6
(4+2t)��6![]() ��3t��4=12+6t6t=12��
��3t��4=12+6t6t=12��
���ı���AMON���������
(3)��OM=ON
��2t=63t��2t=3t6
��t=![]() ��6.
��6.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����M��N�ֱ���������ABCD�ı�CD��CB�ϵĶ��㣬����DM=CN��AM��DN�ཻ�ڵ�E������CE���������εı߳�Ϊ2�����߶�CE����Сֵ��______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����O����ֱ��CD�ĶԳƵ�ΪE������DE��CE��

��1����֤���ı���ODECΪ���Σ�
��2������OE����BC��2![]() ����OE�ij���
����OE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8�֣���ͼ����ƽ��ֱ������ϵ������OAB�Ķ�������ֱ�ΪO��0��0����A��2��1����B��1��-2����
��1����ԭ��OΪλ����������y����Ҳ����OAB��һ��λ�ơ�OA1B1 ��ʹ�����OAB�����Ʊ�Ϊ2��1�����ֱ�д����A��B�Ķ�Ӧ��A1��B1��������
��2����������OAB����ƽ��2����λ��������ƽ��1����λ�����O2A2B2 ����д����A��B�Ķ�Ӧ��A2��B2��������
��3���жϡ�OA1B1���O2A2B2 ���ܷ��ǹ���ijһ��MΪλ�����ĵ�λ��ͼ��������������ͼ�б��λ������M����д����M��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ����ƽ��ֱ������ϵ����ֱ��![]() ��
��![]() ����
����![]() ��ֱ���A��B����������P�ӵ�A��ʼ���߶�AO����ÿ��1����λ���ȵ��ٶ����O�˶���ͬʱ������Q�ӵ�B��ʼ���߶�BA����ÿ��2����λ���ȵ��ٶ����A�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P�˶���ʱ��Ϊt��������
��ֱ���A��B����������P�ӵ�A��ʼ���߶�AO����ÿ��1����λ���ȵ��ٶ����O�˶���ͬʱ������Q�ӵ�B��ʼ���߶�BA����ÿ��2����λ���ȵ��ٶ����A�˶���������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������P�˶���ʱ��Ϊt��������
��1��ֱ��д��A��B��������꣮
��2������APQ����AOB����ʱ����t��ֵ��
��3������APQ�����ΪS��ƽ����λ������S��t֮��ĺ�����ϵʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
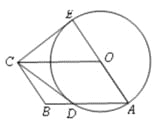
����Ŀ����ͼ���ı���OABC��ƽ���ı��Σ���OΪԲ�ģ�OAΪ�뾶��Բ��AB��D���ӳ� AO����O��E������CD��CE����CE����O�����ߣ�����������⣺
��1����֤��CD����O�����ߣ�
��2����ƽ���ı���OABC�����߳��Ƿ���![]() ����������ƽ���ı���OABC�����.
����������ƽ���ı���OABC�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����E��F�ֱ���ֱ��AB��CD�ϣ���G��H����ֱ��֮�䣬�߶�EF��GH�ཻ�ڵ�O�����С�AEF+��CFE��180�㣬��AEF����1����2������ͼ����ȵĽǹ��У�������

A. 5��B. 6��C. 7��D. 8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ҵΪ�˱���������������![]() ��
��![]() �����ͺŵ���ˮ�����豸��10̨������ͬʱ������ͬ�ɷֵ���ˮ��������
�����ͺŵ���ˮ�����豸��10̨������ͬʱ������ͬ�ɷֵ���ˮ��������![]() ��6̨��
��6̨��![]() ��4̨��112����
��4̨��112����![]() ��4̨��
��4̨��![]() ��6̨����108��Ԫ.
��6̨����108��Ԫ.
��1�����![]() �͡�
�͡�![]() ����ˮ�����豸�ĵ��ۣ�
����ˮ�����豸�ĵ��ۣ�
��2�����˽⣬һ̨![]() ���豸ÿ�¿ɴ�����ˮ220�֣�һ̨
���豸ÿ�¿ɴ�����ˮ220�֣�һ̨![]() ���豸ÿ�¿ɴ�����ˮ190�֣��������ҵ�ƻ��ò�����106��Ԫ���ʽ����������豸������ʹ�������豸ÿ�µ���ˮ������������2005�֣���ͨ������˵�����ַ����Ƿ����.
���豸ÿ�¿ɴ�����ˮ190�֣��������ҵ�ƻ��ò�����106��Ԫ���ʽ����������豸������ʹ�������豸ÿ�µ���ˮ������������2005�֣���ͨ������˵�����ַ����Ƿ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��9�£�ij�ֻ���˾�������¿������ֻ���Ϊ�˵���ijС��ҵ���Ըÿ��ֻ��Ĺ������ù�˾��ijС������Բ���ҵ���������ʾ����飬�涨ÿ��ֻ�ܴ�A�ࣨ����ȥ��������B�ࣨ���ۺ���ȥ��C�ࣨ��ԥ�У���D�ࣨ�϶�������������ѡһ�࣬���Ƴ�������������������ͳ��ͼ����ͼ������������Ϣ����������⣺
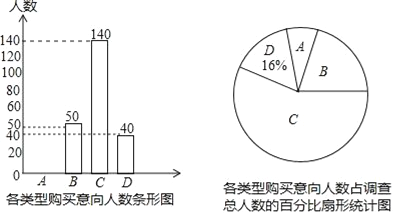
��1������ͳ��ͼ��B���Ӧ�İٷֱ�Ϊ�� ��%���벹ȫ����ͳ��ͼ��
��2������С������4000�ˣ�������Ƹ�С����Լ�ж���������ȥ�����ÿ��ֻ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com