
ЁОЬтФПЁПМИКЮЬНОПЬт
(1)ЗЂЯжЃКдкЦНУцФкЃЌШєBCЃНaЃЌACЃНbЃЌЦфжаaЃОbЃЎ
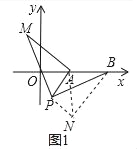
ЕБЕуAдкЯпЖЮBCЩЯЪБ(ШчЭМ1)ЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌзюаЁжЕЮЊЁЁ ЁЁЃЛ
ЕБЕуAдкЯпЖЮBCбгГЄЯпЩЯЪБ(ШчЭМ2)ЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊЁЁ ЁЁЃЎ
(2)гІгУЃКЕуAЮЊЯпЖЮBCЭтвЛЖЏЕуЃЌШчЭМ3ЃЌЗжБ№вдABЁЂACЮЊБпЃЌзїЕШБпЁїABDКЭЕШБпЁїACEЃЌСЌНгCDЁЂBEЃЎ
ЂйжЄУїЃКCDЃНBEЃЛ
ЂкШєBCЃН3ЃЌACЃН1ЃЌдђЯпЖЮCDГЄЖШЕФзюДѓжЕЮЊЁЁ ЁЁЃЎ
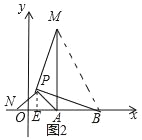
(3)ЭиеЙЃКШчЭМ4ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(5ЃЌ0)ЃЌЕуPЮЊЯпABЭтвЛЖЏЕуЃЌЧвPAЃН2ЃЌPMЃНPBЃЌЁЯBPMЃН90ЁуЃЎЧыжБНгаДГіЯпЖЮAMГЄЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЎ

ЁОД№АИЁП(1)aЉbЃЛ a+bЃЛ(2)ЂйжЄУїМћНтЮіЃЛЂк4ЃЛ(3)ТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуAЮЛгкЯпЖЮBCЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌИљОнЕуAЮЛгкBCЕФбгГЄЯпЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйИљОнЕШБпШ§НЧаЮЕФаджЪЕУЕНADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌЭЦГіЁїCADЁеЁїEABЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНCDЃНBEЃЛ
ЂкгЩгкЯпЖЮCDГЄЕФзюДѓжЕЃНЯпЖЮBEЕФзюДѓжЕЃЌИљОнЃЈ1ЃЉжаЕФНсТлМДПЩЕУЕННсЙћЃЛ
ЃЈ3ЃЉНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌЕУЕНЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНPNЃНPAЃН2ЃЌBNЃНAMЃЌИљОнЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌМДПЩЕУЕНзюДѓжЕЮЊ2![]() +3ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЎ
+3ЃЛШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЎ
(1)ЁпЕБЕуAдкЯпЖЮBCЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюаЁжЕЃЌзюаЁжЕЮЊBCЉACЃЌЁпBCЃНaЃЌACЃНbЃЌЁрBCЉACЃНaЉbЃЌ
ЕБЕуAдкЯпЖЮBCбгГЄЯпЩЯЪБЃЌЯпЖЮABЕФГЄШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊBC+ACЃЌЁпBCЃНaЃЌACЃНbЃЌЁрBC+ACЃНa+bЃЌ
ЙЪД№АИЮЊЃКaЉbЃЌa+bЃЛ
(2)ЂйЁпЁїABDКЭЁїACEЪЧЕШБпШ§НЧаЮЃЌ
ЁрADЃНABЃЌACЃНAEЃЌЁЯBADЃНЁЯCAEЃН60ЁуЃЌ
ЁрЁЯDACЃНЁЯBAEЃЌ
дкЁїACDКЭЁїAEBжаЃЌ ЃЌ
ЃЌ
ЁрЁїACDЁеЁїAEB(SAS)ЃЌ
ЁрCDЃНBEЃЛ
ЂкЁпЯпЖЮCDЕФзюДѓжЕЃНЯпЖЮBEГЄЕФзюДѓжЕЃЌ
гЩ(1)жЊЃЌЕБЯпЖЮBEЕФГЄШЁЕУзюДѓжЕЪБЃЌЕуEдкBCЕФбгГЄЯпЩЯЃЌ
ЁрзюДѓжЕЮЊBC+CEЃНBC+ACЃН4ЃЌ
ЙЪД№АИЮЊЃК4ЃЛ
(3)ЁпНЋЁїAPMШЦзХЕуPЫГЪБеыа§зЊ90ЁуЕУЕНЁїPBNЃЌСЌНгANЃЌ
дђЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPNЃНPAЃН2ЃЌBNЃНAMЃЌ
ЁпAЕФзјБъЮЊ(2ЃЌ0)ЃЌЕуBЕФзјБъЮЊ(5ЃЌ0)ЃЌ
ЁрOAЃН2ЃЌOBЃН5ЃЌ
ЁрABЃН3ЃЌ
ЁрЯпЖЮAMГЄЕФзюДѓжЕЃНЯпЖЮBNГЄЕФзюДѓжЕЃЌ
ЁрЕБNдкЯпЖЮBAЕФбгГЄЯпЪБЃЌЯпЖЮBNШЁЕУзюДѓжЕЃЌ
зюДѓжЕЃНAB+ANЃЌ
ЁпANЃН![]() APЃН2
APЃН2![]() ЃЌ
ЃЌ
ЁрзюДѓжЕЮЊ2![]() +3ЃЛ
+3ЃЛ
ШчЭМ2ЃЌЙ§PзїPEЁЭxжсгкEЃЌСЌНгBEЃЌ
ЁпЁїAPNЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPEЃНAEЃН![]() ЃЌ
ЃЌ
ЁрOEЃНBOЉABЉAEЃН5Љ3Љ![]() ЃН2Љ
ЃН2Љ![]() ЃЌ
ЃЌ
ЁрP(2Љ![]() ЃЌ
ЃЌ![]() )ЃЎ
)ЃЎ
ШчЭМ3жаЃЌИљОнЖдГЦадПЩжЊЃЌЕБЕуPдкЕкЫФЯѓЯоЪБЃЌP(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЪБЃЌвВТњзуЬѕМўЃЎ
)ЪБЃЌвВТњзуЬѕМўЃЎ
злЩЯЪіЃЌТњзуЬѕМўЕФЕуPзјБъ(2Љ![]() ЃЌ
ЃЌ![]() )Лђ(2Љ
)Лђ(2Љ![]() ЃЌЉ
ЃЌЉ![]() )ЃЌAMЕФзюДѓжЕЮЊ2
)ЃЌAMЕФзюДѓжЕЮЊ2![]() +3ЃЎ
+3ЃЎ



 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊНБРјгХаубЇЩњЃЌФГаЃзМБИЙКТђвЛХњЮФОпДќКЭдВЙцзїЮЊНБЦЗЃЌвбжЊЙКТђ1ИіЮФОпДќКЭ2ИідВЙцаш21дЊЃЌЙКТђ2ИіЮФОпДќКЭ3ИідВЙцаш39дЊЁЃ
ЃЈ1ЃЉЧѓЮФОпДќКЭдВЙцЕФЕЅМлЁЃ
ЃЈ2ЃЉбЇаЃзМБИЙКТђЮФОпДќ20ИіЃЌдВЙцШєИЩЃЌЮФОпЕъИјГіСНжжгХЛнЗНАИЃК
ЗНАИвЛЃКЙКТђвЛИіЮФОпДќЛЙЫЭ1ИідВЙцЁЃ
ЗНАИЖўЃКЙКТђдВЙц10ИівдЩЯЪБЃЌГЌГі10ИіЕФВПЗжАДдМлЕФАЫелгХЛнЃЌЮФОпДќВЛДђел.
ЂйЩшЙКТђУцЙцmИіЃЌдђбЁдёЗНАИвЛЕФзмЗбгУЮЊ______ЃЌбЁдёЗНАИЖўЕФзмЗбгУЮЊ______.
ЂкШєбЇаЃЙКТђдВЙц100ИіЃЌдђбЁдёФФжжЗНАИИќКЯЫуЃПЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкГЄЗНаЮABCDжаЃЌ ABЃН8cmЃЌBCЃН12cmЃЌЕуPДгЕуBГіЗЂЃЌвд2cm/УыЕФЫйЖШбиBCЯђЕуCдЫЖЏЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtУыЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌSЁїDCP ЃН ЃЎЃЈгУtЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉШчЭМ1ЃЌЕБtЃН3ЪБЃЌЪдЫЕУїЃКЁїABPЁеЁїDCPЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуPДгЕуBПЊЪМдЫЖЏЕФЭЌЪБЃЌЕуQДгЕуCГіЗЂЃЌвдv cm/УыЕФЫйЖШбиCDЯђЕуDдЫЖЏЃЌЪЧЗёДцдкетбљvЕФжЕЃЌЪЙЕУЁїABPгыЁїPQCШЋЕШЃПШєДцдкЃЌЧыЧѓГіvЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъОЯњвЛжжГЩБОЮЊУПЧЇПЫ40дЊЕФЫЎВњЦЗЃЌОнЪаГЁЗжЮіЃЌШєАДУПЧЇПЫ50дЊЯњЪлЃЌвЛИідТФмЪлГі500ЧЇПЫЃЎШєЯњЪлМлУПеЧ1дЊЃЌдђдТЯњЪлСПМѕЩй10ЧЇПЫЃЎ
ЃЈ1ЃЉвЊЪЙдТЯњЪлРћШѓДяЕНзюДѓЃЌЯњЪлЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ЃЈ2ЃЉвЊЪЙдТЯњЪлРћШѓВЛЕЭгк8000дЊЃЌЧыНсКЯЭМЯѓЫЕУїЯњЪлЕЅМлгІШчКЮЖЈЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКНХФЮоШЫЛњМзДгКЃАЮ![]() ДІГіЗЂЃЌвд
ДІГіЗЂЃЌвд![]() дШЫйЧІжБЩЯЩ§ЃЌгыДЫЭЌЪБЃЌКНХФЮоШЫЛњввДгКЃАЮ
дШЫйЧІжБЩЯЩ§ЃЌгыДЫЭЌЪБЃЌКНХФЮоШЫЛњввДгКЃАЮ![]() ДІГіЗЂЃЌвд
ДІГіЗЂЃЌвд![]() дШЫйЧІжБЩЯЩ§ЃЎЩшЮоШЫЛњЩЯЩ§ЪБМфЮЊ
дШЫйЧІжБЩЯЩ§ЃЎЩшЮоШЫЛњЩЯЩ§ЪБМфЮЊ![]() ЃЌЮоШЫЛњМзЁЂввЫљдкЮЛжУЕФИпЖШЗжБ№ЮЊ
ЃЌЮоШЫЛњМзЁЂввЫљдкЮЛжУЕФИпЖШЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]()
ЃЈ1ЃЉИљОнЬтвтЃЌЬюаДЯТБэЃК
ЩЯЩ§ЪБМф | 5 | 10 |
|
| 25 |
| |
| 60 |
|
ЃЈ2ЃЉЧыФуЗжБ№аДГі![]() ЁЂ
ЁЂ![]() гы
гы![]() ЕФЙиЯЕЪНЃЛ
ЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкФГЪБПЬСНМмЮоШЫЛњФмЗёЮЛгкЭЌвЛИпЖШЃПШєФмЃЌЧѓЮоШЫЛњЩЯЩ§ЕФЪБМфКЭЫљдкИпЖШЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЁЯAPB=30ЁуЃЌOP=3cmЃЌЁбOЕФАыОЖЮЊ1cmЃЌШєдВаФOбизХBPЕФЗНЯђдкжБЯпBPЩЯвЦЖЏЃЎ
ЃЈЂёЃЉЕБдВаФOвЦЖЏЕФОрРыЮЊ1cmЪБЃЌдђЁбOгыжБЯпPAЕФЮЛжУЙиЯЕЪЧ ЃЎ
ЃЈЂђЃЉШєдВаФOЕФвЦЖЏОрРыЪЧdЃЌЕБЁбOгыжБЯпPAЯрНЛЪБЃЌдђdЕФШЁжЕЗЖЮЇЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМгЧПбЇЩњЕФАВШЋвтЪЖЃЌФГаЃзщжЏСЫбЇЩњВЮМгАВШЋжЊЪЖОКШќЃЌДгжаГщШЁСЫВПЗжбЇЩњГЩМЈНјааЭГМЦЃЌВЂАДееГЩМЈДгЕЭЕНИпЗжГЩAЃЌBЃЌCЃЌDЃЌEЮхИіаЁзщЃЌЛцжЦЭГМЦЭМШчЯТЃЈЮДЭъГЩЃЉЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉбљБОШнСПЮЊЁЁЁЁЃЌЦЕЪ§ЗжВМжБЗНЭМжаaЃНЁЁЁЁЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаDаЁзщЫљЖдгІЕФЩШаЮдВаФНЧЮЊnЁуЃЌЧѓnЕФжЕВЂВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉШєГЩМЈдк80ЗжвдЩЯЃЈВЛКЌ80ЗжЃЉЮЊгХауЃЌШЋаЃЙВга2000УћбЇЩњЃЌЙРМЦГЩМЈгХауЕФбЇЩњгаЖрЩйУћЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаЫФЯюЕїВщжаЃЌЗНЪНе§ШЗЕФЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. ЖдФГРрбЬЛЈБЌжёШМЗХАВШЋЧщПіЃЌВЩгУШЋУцЕїВщЕФЗНЪН
B. СЫНтФГАрЭЌбЇУПжмЖЭСЖЕФЪБЮЪЃЌВЩгУШЋУцЕїВщЕФЗНЪН
C. ЮЊБЃжЄдЫдиЛ№М§ЕФГЩЙІЗЂЩфЃЌЖдЦфЫљгаЕФСуВПМўВЩгУГщбљЕїВщЕФЗНЪН
D. СЫНтФГЪЁжабЇЩњAЪгСІЧщПіЃЌВЩгУШЋУцЕїВщЕФЗНЪН
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁбOЪЧRtЁїABCЕФЭтНгдВЃЌЁЯABC=90ЁуЃЌЯвBD=BAЃЌAC=13ЃЌBC=5ЃЌBEЁЭDCНЛDCЕФбгГЄЯпгкЕуEЃЎ

ЃЈ1ЃЉЧѓжЄЃКCBЪЧЁЯECAЕФНЧЦНЗжЯпЃЛ
ЃЈ2ЃЉЧѓDEЕФГЄЃЛ
ЃЈ3ЃЉЧѓжЄЃКBEЪЧЁбOЕФЧаЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com