练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法：①内错角相等；②两条直线不平行必相交；③过一点有且只有一条直线与已知直线垂直；④平行于同一条直线的两条直线互相平行． 其中错误的有（ ）．

    A.1个；B.2个；C.3个；D.4个．

    【答案】C

    【解析】

    由题意根据相交线和平行线的性质，分别进行分析判断即可.

    解：①两直线平行，内错角相等，①错误；

    ②在同一平面内，两条直线不平行必相交，②错误；

    ③在同一平面内，过一点有且只有一条直线与已知直线垂直，③错误；

    ④平行于同一条直线的两条直线互相平行，④正确．

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，△ABC中，AB=AC，∠ABC=60°，AD=CE，求∠BPD的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

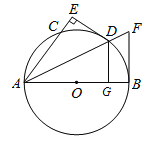
    【题目】如图，已知AB为⊙O直径，D是的中点，DE⊥AC交AC的延长线于E，⊙O的切线交AD的延长线于F．

    （1）求证：直线DE与⊙O相切；

    （2）已知DG⊥AB且DE=4，⊙O的半径为5，求tan∠F的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题情境】

    在△ABC中，AB=AC，点P为BC所在直线上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．当P在BC边上时（如图1），求证：PD+PE=CF．

    图① 图② 图③

    证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．（不要证明）

    【变式探究】

    当点P在CB延长线上时，其余条件不变（如图3）.试探索PD、PE、CF之间的数量关系并说明理由.

    请运用上述解答中所积累的经验和方法完成下列两题：

    【结论运用】

    如图4，将长方形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；

    【迁移拓展】

    在直角坐标系中.直线l1：y=与直线l2：y=2x+4相交于点A，直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC，∠C=90°，∠ABC=40°，按以下步骤作图：

    ①以点A为圆心，小于AC的长为半径．画弧，分别交AB、AC于点E、F；

    ②分别以点E、F为圆心，大于EF的长为半径画弧，两弧相交于点G；

    ③作射线AG，交BC边于点D，则∠ADC的度数为________．

    【答案】65°

    【解析】由题意可知，所作的射线AG是∠BAC的角平分线.

    ∵在△ABC中，∠C=90°，∠ABC=40°，

    ∴∠BAC=180°-90°-40°=50°，

    ∴∠CAD=∠BAC=25°，

    ∴∠ADC=180°-90°-25°=65°.

    【题型】填空题
    【结束】
    13

    【题目】如图所示，已知线段AB，∠α，∠β，分别过A、B作∠CAB=∠α，∠CBA=∠β．（不写作法，保留作图痕迹）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校为了解七年级男生体质健康情况，随机抽取若干名男生进行测试，测试结果分为优秀、良好、合格、不合格四个等级，统计整理数据并绘制图1、图2两幅不完整的统计图，请根据图中信息回答下列问题：

    （1）本次接收随机抽样调查的男生人数为　 　人，扇形统计图中“良好”所对应的圆心角的度数为　 　；

    （2）补全条形统计图中“优秀”的空缺部分；

    （3）若该校七年级共有男生480人，请估计全年级男生体质健康状况达到“良好”的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底M处出发，向前走3米到达A处，测得树顶端E的仰角为30°，他又继续走下台阶到达C处，测得树的顶端E的仰角是60°，再继续向前走到大树底D处，测得食堂楼顶N的仰角为45°．已知A点离地面的高度AB=2米，∠BCA=30°，且B、C、D三点在同一直线上．

    （1）求树DE的高度；

    （2）求食堂MN的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛，初赛后对选手成绩进行了整理，分成5个小组（x表示成绩，单位：分），A组：75≤x＜80；B组：80≤x＜85；C组：85≤x＜90；D组：90≤x＜95；E组：95≤x＜100．并绘制出如图两幅不完整的统计图．

    请根据图中信息，解答下列问题：

    （1）参加初赛的选手共有 名，请补全频数分布直方图；

    （2）扇形统计图中，C组对应的圆心角是多少度？E组人数占参赛选手的百分比是多少？

    （3）学校准备组成8人的代表队参加市级决赛，E组6名选手直接进入代表队，现要从D组中的两名男生和两名女生中，随机选取两名选手进入代表队，请用列表或画树状图的方法，求恰好选中一名男生和一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC中，AB=AC．D是直线BC上的点，DE⊥AB．垂足是点E．

    （1）如图①，当∠A=50，点D在线段BC延长线上时，∠EOB=____；

    （2）如图②，当∠A=50，点D在线段BC上时，∠EDB=____；

    （3）如图③，当∠A=110，点D在线段BC上时，∠EDB=____；

    （4）结合（1）、（2）、（3）的结果可以发现，∠EDB与∠A的数量关系是∠EDB=____∠A．

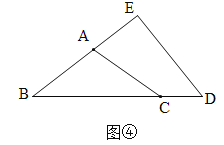
    （5）按你发现的规律，当点D在线段BC延长线上，∠EDB=50，其余条件不变时如图④，不用计算，直接填空∠BAC=____．

    查看答案和解析>>

    同步练习册答案