
【题目】【问题情境】
在△ABC中,AB=AC,点P为BC所在直线上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.当P在BC边上时(如图1),求证:PD+PE=CF.

图① 图② 图③
证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.(不要证明)
【变式探究】
当点P在CB延长线上时,其余条件不变(如图3).试探索PD、PE、CF之间的数量关系并说明理由.
请运用上述解答中所积累的经验和方法完成下列两题:
【结论运用】
如图4,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;

【迁移拓展】
在直角坐标系中.直线l1:y=![]() 与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.
与直线l2:y=2x+4相交于点A,直线l1、l2与x轴分别交于点B、点C.点P是直线l2上一个动点,若点P到直线l1的距离为1.求点P的坐标.

【答案】【变式探究】:详见解析;【结论运用】:4;【迁移拓展】:P1的坐标为(![]() ,3)或(
,3)或(![]() ,5)
,5)
【解析】试题分析:【变式探究】按照【问题情境】的证明思路即可解决问题.
【结论运用】过![]() 作
作![]() 利用问题情境中的结论可得
利用问题情境中的结论可得![]() ,易证
,易证![]() 只需求即可.
只需求即可.
【迁移拓展】分成两种情况进行讨论.
试题解析:【变式探究】:连接![]()
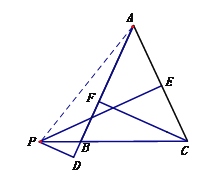
∵PD⊥AB,PE⊥AC,CF⊥AB,
![]()
![]()
![]()
![]()
【结论运用】过![]() 作
作![]() 垂足为
垂足为![]() ,如图④,
,如图④,
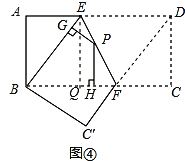
∵四边形![]() 是长方形,
是长方形, ![]()
![]()
由折叠可得: ![]()
![]()
![]()
![]()
![]()
∴四边形![]() 是长方形.
是长方形. ![]()
∵AD∥BC, ![]()
![]()
由问题情境中的结论可得: ![]()
![]() 的值为4.
的值为4.
【迁移拓展】
由题意得: ![]()
![]()
![]()
![]()
(1)由结论得: ![]()
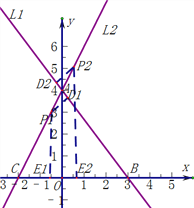
![]()
即点![]() 的纵坐标为3,
的纵坐标为3,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =3 ,
=3 ,
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()
(2) 由结论得: ![]()
![]() 即点
即点![]() 的纵坐标为5,
的纵坐标为5,
又点![]() 在直线l2上 ∴
在直线l2上 ∴![]() =5.
=5.
∴![]() .
.
即点![]() 的坐标为
的坐标为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为cm2 . 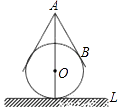
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题:

(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的解题过程:
用公式法解下列方程:
(1)2x2﹣3x﹣2=0.
解:a=___,b=___,c=___.
b2﹣4ac=___=___>0.
![]() =____=___,
=____=___,
x1=__,x2=___.
(2)x(2x﹣![]() )=
)=![]() x﹣3.
x﹣3.
解:整理,得___.
a=__,b=___,c=___.
b2﹣4ac=___=___.
![]() =_____=____,
=_____=____,
x1=x2=__.
(3)(x﹣2)2=x﹣3.
解:整理,得______.
a=___,b=___,c=___.
b2﹣4ac=___=___<0.
方程___实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①内错角相等;②两条直线不平行必相交;③过一点有且只有一条直线与已知直线垂直;④平行于同一条直线的两条直线互相平行. 其中错误的有( ).
A.1个;B.2个;C.3个;D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.试说明:AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
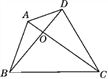
解:在△OAB中有OA+OB>AB,
在△OAD中有______________,
在△ODC中有______________,
在△________中有______________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,
即________________________.
∴AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com