
【题目】已知:在△ABC中,AB=AC.D是直线BC上的点,DE⊥AB.垂足是点E.
(1)如图①,当∠A=50![]() ,点D在线段BC延长线上时,∠EOB=____;
,点D在线段BC延长线上时,∠EOB=____;
(2)如图②,当∠A=50![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;
(3)如图③,当∠A=110![]() ,点D在线段BC上时,∠EDB=____;
,点D在线段BC上时,∠EDB=____;

(4)结合(1)、(2)、(3)的结果可以发现,∠EDB与∠A的数量关系是∠EDB=____∠A.
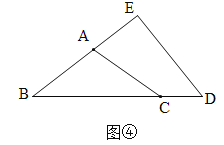
(5)按你发现的规律,当点D在线段BC延长线上,∠EDB=50![]() ,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
,其余条件不变时如图④,不用计算,直接填空∠BAC=____.
【答案】(1)25°;(2)25°;(3)55°;(4)![]() ;(5)100°.
;(5)100°.
【解析】试题分析:(1)在△ABC中,由AB=AC,∠A=50![]() ,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
(2)在△ABC中,由AB=AC,∠A=50![]() ,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
(3)在△ABC中,由AB=AC,∠A=50![]() ,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
,可得∠B=65°,由DE⊥AB,∠BED=90°,可求得∠EDB;
(4)观察(1)(2)(3)的结果即可得∠EDB与∠A的数量关系;
(5)由(4)即可直接得出结果.
试题解析:(1)∵AB=AC,
∴∠B=∠C,
∵∠A=50![]() ,
,
∴∠B=65°,
∵DE⊥AB,
∴∠BED=90°,
∴∠EDB=90°-∠B=25°;
故答案为:25°;
(2)∵AB=AC,
∴∠B=∠C,
∵∠A=50![]() ,
,
∴∠B=65°,
∵DE⊥AB,
∴∠BED=90°,
∴∠EDB=90°-∠B=25°;
故答案为:25°;
(3)∵AB=AC,
∴∠B=∠C,
∵∠A=110![]() ,
,
∴∠B=35°,
∵DE⊥AB,
∴∠BED=90°,
∴∠EDB=90°-∠B=55°;
故答案为:55°;
(4)由(1)(2)(3)可得![]() ∠A.
∠A.
故答案为: ![]() ;
;
(5)∵![]() ∠A,∠EDB=50
∠A,∠EDB=50![]() ,
,
∴∠A=100°.


科目:初中数学 来源: 题型:
【题目】下列说法:①内错角相等;②两条直线不平行必相交;③过一点有且只有一条直线与已知直线垂直;④平行于同一条直线的两条直线互相平行. 其中错误的有( ).
A.1个;B.2个;C.3个;D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数![]() 的图象于点B,AB=
的图象于点B,AB=![]() .
.
(1)求反比例函数的解析式;
(2)若P(![]() ,
, ![]() )、Q(
)、Q(![]() ,
, ![]() )是该反比例函数图象上的两点,且
)是该反比例函数图象上的两点,且![]() 时,
时, ![]() ,指出点P、Q各位于哪个象限?并简要说明理由.
,指出点P、Q各位于哪个象限?并简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是任意四边形,AC与BD交于点O.试说明:AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
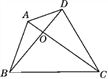
解:在△OAB中有OA+OB>AB,
在△OAD中有______________,
在△ODC中有______________,
在△________中有______________,
∴OA+OB+OA+OD+OD+OC+OB+OC>AB+AD+CD+BC,
即________________________.
∴AC+BD>![]() (AB+BC+CD+DA).
(AB+BC+CD+DA).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式配成完全平方式:
①x2+6x+______=(x+____)2 ②x2-5x+_____=(x-____)2;
③x2+ x+______=(x+____)2 ④x2-9x+_____=(x-____)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的高,D是AM上的点,以CD为一边,在CD的下方作等边△CDE,连结BE.
(1)填空:∠ACB=____;∠CAM=____;
(2)求证:△AOC≌△BEC;
(3)延长BE交射线AM于点F,请把图形补充完整,并求∠BFM的度数;
(4)当动点D在射线AM上,且在BC下方时,设直线BE与直线AM的交点为F.∠BFM的大小是否发生变化?若不变,请在备用图中面出图形,井直接写出∠BFM的度数;若变化,请写出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学库存若干套桌椅,准备修理后支援贫困山区学校。现有甲、乙两木工组,甲每天修理桌椅16套,乙每天修桌椅比甲多8套,甲单独修完这些桌椅比乙单独修完多用20天,学校每天付甲组80元修理费,付乙组120元修理费。
(1)该中学库存多少套桌椅?
(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天10元生活补助费,现有三种修理方案:a、由甲单独修理;b、由乙单独修理;c、甲、乙合作同时修理。你认为哪种方案省时又省钱?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com