
����Ŀ����ͼ���ڵȱߡ�ABC�����߶�AMΪBC���ϵĸ���D��AM�ϵĵ�����CDΪһ������CD���·����ȱߡ�CDE������BE��
��1���������ACB=____����CAM=____��
��2����֤����AOC�ա�BEC��
��3���ӳ�BE������AM�ڵ�F�����ͼ�β��������������BFM�Ķ�����
��4��������D������AM��������BC�·�ʱ����ֱ��BE��ֱ��AM�Ľ���ΪF����BFM�Ĵ�С�Ƿ����仯�������������ڱ���ͼ�����ͼ������ֱ��д����BFM�Ķ��������仯����д���仯������

���𰸡���1��60�㣬30�㣻��2���𰸼���������3��60�㣻��4����BFM��60�㣮
�������������������1�����ݵȱ������ε����ʼ��ɽ��н��
��2�����ݵȱ������ε����ʾͿ��Եó�AC=AC��DC=EC����ACB=��DCE=60�����ɵ�ʽ�����ʾͿ��ԡ�BCE=��ACD������SAS�Ϳ��Եó���ADC�ա�BEC��
��3����ȫͼ�Σ�����ADC�ա�BEC�á�CAM=��CBE=30��,���������ڽǺͶ���������á�BFM�Ķ�����
��4��������Ӧͼ�Σ���֪����D���߶�AM���ӳ���������BC�·�ʱ����ͼ�����Եó���ACD�ա�BCE�������õ���CBE=��CAD=30�����ݴ˵ó����ۣ�
���������(1)����ABC�ǵȱ������Σ�
���ACB=60����
���߶�AMΪBC���ϵĸߣ�
���CAM=![]() ��BAC=30����
��BAC=30����
�ʴ�Ϊ��60��30����
��3������ABC����DEC���ǵȱ������Σ�
��AC=BC,CD=CE,��ACB=��DCE=60����
���ACD+��DCB=��DCB+��BCE��
���ACD=��BCE.
����ADC����BEC��
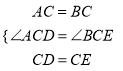 ��
��
����ACD����BCE(SAS)��
��3����ȫͼ�����£�
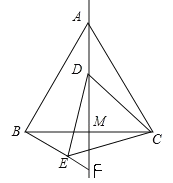
�ɣ�1����2���á�CAM=30������ADC�ա�BEC��
���CBE=��CAM=30����
�ߡ�BMF=90����
���BFM=60����
��4��������D������AM�ϣ�����BC�·�ʱ������ͼ�����£�
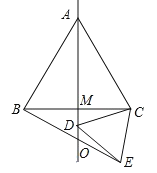
����ABC����DEC���ǵȱ������Σ�
��AC=BC,CD=CE,��ACB=��DCE=60����
���ACB+��DCB=��DCB+��DCE��
���ACD=��BCE��
����ACD����BCE��
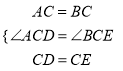 ��
��
����ACD����BCE(SAS)��
���CBE=��CAD=30����
�֡ߡ�AMC=��BMO��
���AOB=��ACB=60��.
������D������AM��ʱ,��AOBΪ��ֵ60��.


 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˽����꼶�������ʽ�������������ȡ�������������в��ԣ����Խ����Ϊ���㡢���á��ϸ��ϸ��ĸ��ȼ���ͳ���������ݲ�����ͼ1��ͼ2������������ͳ��ͼ�������ͼ����Ϣ�ش��������⣺

��1�����ν�����������������������Ϊ�� ���ˣ�����ͳ��ͼ�С����á�����Ӧ��Բ�ĽǵĶ���Ϊ�� ����
��2����ȫ����ͳ��ͼ�С����㡱�Ŀ�ȱ���֣�
��3������У���꼶��������480�ˣ������ȫ�꼶�������ʽ���״���ﵽ�����á���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֻ������̹����ף�������Ʒ���ֻ��� 100 ��.
��1����֪�����ֻ�ÿ������ 1500 Ԫ���ۼ� 2000 Ԫ�������ֻ�ÿ������ 3500 Ԫ���ۼ� 4500 Ԫ���ɹ��������ֻ�ǡ������ 27 ��Ԫ .���������ֻ�ȫ����������̹���������Ԫ��
��2���Ѿ������ף��������ֻ���һ�������� 5000 Ԫ�������̰Ѽ����ֻ��Ӽ� 50%��Ϊ��ۣ������ֻ��Ӽ� 40%��Ϊ���.
�� A��B ��������ѡһ������
A����ʵ�ʳ���ʱ����ͬʱ����ף����ֻ���һ����������ۣ���ʱ�����̿ɻ��� 1570 Ԫ.��ף��������ֻ�ÿ���Ľ���.
B�������̲ɹ������ֻ��������������ֻ������� 1.5 ��.�����������ã�����ڰ���۽������۵�����£������ֻ��ܿ����꣬���ż����ֻ������ 10 ������۵İ���ȫ������.����������У������̻�õ�������Ϊ 42.5%.��ף��������ֻ�ÿ���Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����x����2��һԪ���η���ax2��8��12��a�Ľ⣬��a��ֵ�ǣ� ��
A.��20B.4C.��3D.��10
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
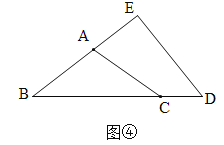
����Ŀ����֪���ڡ�ABC����AB=AC��D��ֱ��BC�ϵĵ���DE��AB�������ǵ�E��
��1����ͼ��������A=50![]() ����D���߶�BC�ӳ�����ʱ����EOB=____��
����D���߶�BC�ӳ�����ʱ����EOB=____��
��2����ͼ��������A=50![]() ����D���߶�BC��ʱ����EDB=____��
����D���߶�BC��ʱ����EDB=____��
��3����ͼ��������A=110![]() ����D���߶�BC��ʱ����EDB=____��
����D���߶�BC��ʱ����EDB=____��

��4�������1������2������3���Ľ�����Է�������EDB���A��������ϵ�ǡ�EDB=____��A��
��5�����㷢�ֵĹ���������D���߶�BC�ӳ���������EDB=50![]() ��������������ʱ��ͼ�������ü�����ֱ����ա�BAC=____��
��������������ʱ��ͼ�������ü�����ֱ����ա�BAC=____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ���Rt��ABC��б��AB��ֱ�DZ�ACΪ���������ȱ���ABD����ACE��FΪAB���е㣬DE��AB�ཻ�ڵ�G������BAC=30�������н��ۣ���EF��AC�����ı���ADFEΪ���Σ���AD=4AG���ܡ�DBF�ա�EFA��������ȷ���۵�����ǣ�������

A. �ڢ� B. �٢� C. �ڢۢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
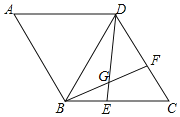
����Ŀ����ͼ��������ABCD�У�AB=BD����E��F�ֱ���BC��CD���ϣ���CE=DF��BF��DE���ڵ�G����BG=2��DG=4����CD��Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c����ABC�����ߣ�����![]() ����a��b��c��12.
����a��b��c��12.
(1)����a��b��c��ֵ��
(2)������ABC�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com