
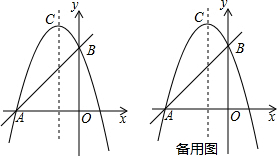
分析 (1)先根据直线y=x+3求出A、B两点的坐标,然后将它们代入抛物线中即可求出待定系数的值,根据抛物线的解析式可求出C的坐标;
(2)分别从AB=BQ,AQ=BQ,AB=AQ三方面去分析,注意抓住线段的求解方法,借助于方程求解即可求得答案.
解答 解:(1)由经过点A,B的直线的表达式为y=x+3.可知A(-3,0),B(0,3),
∵抛物线y=-x2+bx+c交x轴于点A,交y轴于点B,
∴$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$,
解得:b=-2,c=3,
∴抛物线的解析式为:y=-x2-2x+3,
∵y=-x2-2x+3=-(x+1)2+4,
∴顶点C(-1,4);
(2)存在;
理由:∵A(-3,0),B(0,3),
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∵Q在直线x=-1上,
∴设Q(-1,n),
∵点A,B,Q构成的三角形是以AB为腰的等腰三角形,
①当AQ=AB=3$\sqrt{2}$,
∴22+n2=(3$\sqrt{2}$)2,
∴n=$\sqrt{14}$,或n=-$\sqrt{14}$,
②当BQ=AB=3$\sqrt{2}$,
∴12+(3-n)2=(3$\sqrt{2}$)2
∴n=3+$\sqrt{17}$,或n=3-$\sqrt{17}$,
∴Q(-1,$\sqrt{14}$);(-1,-$\sqrt{14}$);(-1,3+$\sqrt{17}$)或(-1,3-$\sqrt{17}$).
点评 此题考查了待定系数法求二次函数的解析式与等腰三角形的性质等知识.此题难度适中,注意分类讨论思想,方程思想与数形结合思想的应用是解此题的关键,还要注意别漏.


科目:初中数学 来源: 题型:解答题
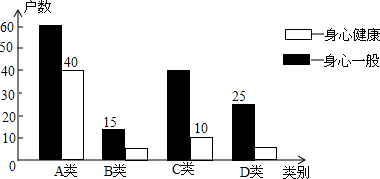
| 类别 | 现状 | 户数 | 比例 |
| A类 | 父母常年在外打工,孩子留在老家由老人照顾 | 100 | |
| B类 | 父母常年在外打工,孩子带在身边 | 20 | 10% |
| C类 | 父母就近在城镇打工,晚上回家照顾孩子 | 50 | |
| D类 | 父母在家务农,并照顾孩子 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
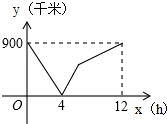 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,两车的距离y(千米)与慢车行驶的时间为x(小时)之间的函数关系如图所示,则快车到达乙地时慢车离乙地距离为450千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com