Question

如果抛物线y=x²-（k-1）x-k-1与x轴的交点为A、B，顶点C，那么三角形ABC的面积的最小值是（ ）
A．1
B．2
C．3
D．4

Answer 1

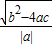
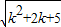
【答案】分析：根据一元二次方程根与系数的关系，可以求得AB==，再根据顶点的纵坐标公式求得点C的纵坐标，显然要求三角形ABC的面积的最小值，即求k²+2k+5的最小值，从而求解．
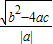
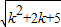
解答：解：∵AB==，点C的纵坐标是-（k²+2k+5），
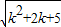
∴三角形ABC的面积=××（k²+2k+5），
又k²+2k+5的最小值是4，
则三角形ABC的面积的最小值是1．
故选A．
点评：此题综合运用了坐标轴上两点间的距离公式、一元二次方程根与系数之间的关系以及二次函数的最值问题．