练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示,A、B 两点分别位于一个池塘的两端，小明想用绳子测量A、B 间的距离，但绳子不够长,请你利用三角形全等的相关知识帮他设计一种方案测量出A、B间的距离,写出具体的方案,并解释其中的道理,

    【答案】见解析.

    【解析】

    根据全等三角形判定和性质可得：构造出△ABC≌△DEC（SAS）.

    例如，如图.

    （1）先在地上取一个可以直接到达A点和B点的点C；

    （2）连接AC并延长到点D，使得CD=AC；

    （3）连接BC并延长到点E，使得CE=BC；

    （4）连接DE，并测量出它的长度.

    DE的长度就是A、B间的距离.

    理由如下：

    在△ABC和△DEC中，

    因为AC=DC，∠ACB=∠DCE，BC=EC.

    所以△ABC≌△DEC（SAS）.

    所以AB=DE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，O是等边△ABC内一点，连接OA、OB、OC，且OA=3，OB=4，OC=5，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．求：

    ①旋转角的度数；

    ②线段OD的长；

    ③∠BDC的度数．

    （2）如图2所示，O是等腰直角△ABC（∠ABC=90°）内一点，连接OA、OB、OC，将△BAO绕点B顺时针旋转后得到△BCD，连接OD．当OA、OB、OC满足什么条件时，∠ODC=90°？请给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一个零件的形状如图所示，按规定∠A应等于90°，∠B、∠D应分别是20°和30°.

    （1）李叔叔量得∠BCD=142°，根据李叔叔量得的结果，你能断定这个零件是否合格？请解释你的结论.

    （2）你知道∠B、∠D、∠BCD三角之间有何关系吗？请写出你的结论（不需说明理由）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD的边平行于坐标轴，对角线BD经过坐标原点，点C在反比例函数y=的图象上．若点A的坐标为（﹣2，﹣2），则k=（　　）

    A. 2 B. 4 C. 8 D. 16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠BAC=90°，AB=AC，点D为BC的中点，点E、F分别在边AB和边AC上，且∠EDF=90°，则下列结论一定成立的是_______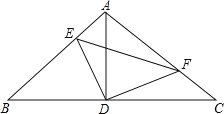

    ①△ADF≌△BDE

    ②S四边形AEDF=S△ABC

    ③BE+CF=AD

    ④EF=AD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】暑假降至，丹尼斯大卖场为回馈新老顾客，进行有奖促销活动活动. 活动规定：购买500元的商品就可以获得一次转转盘的机会（转盘分为5个区域，分别是特等奖、一等奖、二等奖、三等奖、不获奖），转盘指针停在哪个获奖区域就可以得到该区域相应等级奖品一件（如果指针恰好停在分割线上，那么重转一次，直到指针指向某一区域为止）. 大卖场工作人员在制作转盘时，将各扇形区域圆心角（不完全）分配如下表：

    奖次

    特等奖

    一等奖

    二等奖

    三等奖

    不获奖

    圆心角

    _________

    促销公告：凡购买我大卖场商品500元均有可能获得下列奖品:

    特等奖：山地越野自行车一辆 一等奖：双肩背包一个

    二等奖：洗衣液一桶 三等奖：抽纸一盒

    根据以上信息，解答下列问题：

    （1）求不获奖的扇形区域圆心角度数是多少？

    （2）求获得双肩背包的概率是多少？

    （3）甲顾客购物520元，求他获奖的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形ABCD的位置如图所示，解答下列问题：

    (1)将四边形ABCD先向左平移4格，再向下平移6格，得到四边形A1B1C1D1，画出平移后的四边形A1B1C1D1；

    (2)将四边形A1B1C1D1绕点A1逆时针旋转90°得到四边形A1B2C2D2，画出旋转后的四边形A1B2C2D2.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．

    （1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；

    （2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；

    （3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD四条边上的中点分别为E．F．G．H，顺次连接EF．FG．GH．HE，得到四边形EFGH（即四边形ABCD的中点四边形）．

    （1）四边形EFGH的形状是 ，证明你的结论．

    （2）当四边形ABCD的对角线满足 条件时，四边形EFGH是矩形；

    （3）结合问题（2），请做出图形并且证明

    查看答案和解析>>

    同步练习册答案