
【题目】如图是某校在慈善爱心捐款活动中的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查.
(1)在抽取的样本中,捐款金额的平均数、中位数、众数各是多少?
(2)若该校九年级共有200人捐款,请你估计全校捐款的总金额约为多少元?

【答案】(1)捐款金额的平均数是17.4元,中位数为20元,众数是20元;(2)13920元.
【解析】
(1)由图2的数据根据平均数公式,中位数、众数定义即可得出答案.
(2)由图1知:九年级捐款人数占总捐款人数的百分比为25%,从而求出全校捐款人数,用这个捐款人数乘以捐款平均数即可求得答案.
解:(1)由图2可知:
捐款金额:5,10,15,20,25,
捐款人数:4,8,10,16,12,
∴捐款金额的平均数为:![]() =17.4(元),
=17.4(元),
捐款金额的中位数为:20元,
捐款金额的众数为:20元,
答: 捐款金额的平均数是17.4元,中位数为20元,众数是20元.
(2)由图1知:
九年级捐款人数占总捐款人数的百分比为:
1-35%-40%=25%,
∴全校捐款人数为:200÷25%=800(人),
∴全校捐款的总金额约为:800×17.4=13920(元),
答:全校捐款的总金额约为13920元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示:有边长为a的正方形A类卡片、边长为b的正方形B类卡片、长和宽分别为a、b的长方形C类卡片各若干张,如果要拼一个边长分别为![]() 、
、![]() 的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )
的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少? .
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;方法二: .
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2;(m﹣n)2; mm
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,求(a﹣b)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为![]() ,宽为b
,宽为b![]() 的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
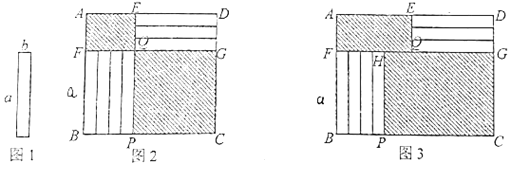
(1)如图2,点E、Q、P在同一直线上,点F、Q、G在同一直线上,右下角与左上角的阴影部分的面积的差为____________(用含![]() 、
、![]() 的代数式表示),矩形ABCD的面积为____________(用含
的代数式表示),矩形ABCD的面积为____________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图3,点F、H、Q、G在同一直线上,设右下角与左上角的阴影部分的面积的差为S,![]() .
.
①用![]() 、
、![]() 、
、![]() 的代数式表示AE;
的代数式表示AE;
②当BC的长度变化时,按照同样的放置方式,S始终保持不变,那么![]() 、
、![]() 必须满足什么条件?
必须满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
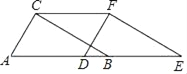
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,将△ABC沿AB方向向右平移得到△DEF,若AE=8cm.
(1)求△ABC向右平移的距离AD的长;
(2)求四边形AEFC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视举办的《中国诗词大会》受到广大的关注.深圳某中学学生会就《中国诗词大会》节目的喜爱程度,在校内进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形和条形统计图,请结合图中所给信息解答下列问题:

(1)本次被调查的对象共有 人;被调查者“不太喜欢”有 人;
(2)将扇形统计图和条形统计图补充完整;
(3)假设这所学校有1500名学生,请据此估计“比较喜欢”的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com