
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
【答案】(1) a1=![]() .(2) a2=
.(2) a2=![]() ’ (3) an=
’ (3) an=![]() .
.
【解析】分析:(1)设PQ与![]() 交于点D,连接
交于点D,连接![]() ,得出OD=
,得出OD= ![]() -O
-O![]() ,用含
,用含![]() 的代数式表示OD,在△O
的代数式表示OD,在△O![]() D中,根据勾股定理求出正三角形的边长
D中,根据勾股定理求出正三角形的边长![]() ;(2)设PQ与
;(2)设PQ与![]()
![]() 交于点E,连接
交于点E,连接![]() O,得出OE=
O,得出OE=![]() E-O
E-O![]() ,用含
,用含![]() 的代数式表示OE,在△O
的代数式表示OE,在△O![]() E中,根据勾股定理求出正三角形的边长
E中,根据勾股定理求出正三角形的边长![]() ;(3)设PQ与
;(3)设PQ与![]()
![]() 交于点F,连接
交于点F,连接![]() O,得出OF=
O,得出OF=![]() F-O
F-O![]() ,用含an的代数式表示OF,在△O
,用含an的代数式表示OF,在△O![]() F中,根据勾股定理求出正三角形的边长an.
F中,根据勾股定理求出正三角形的边长an.
本题解析:
(1)易知△A1B1C1的高为![]() ,则边长为
,则边长为![]() ,
,
∴a1=![]() .
.
(2)设△A1B1C1的高为h,则A2O=1-h,连结B2O,设B2C2与PQ交于点F,则有OF=2h-1.
∵B2O2=OF2+B2F2,∴1=(2h-1)2+![]() .
.
∵h=![]() a2,∴1=(
a2,∴1=(![]() a2-1)2+
a2-1)2+![]() a22,
a22,
解得a2=![]() .
.
(3)同(2),连结BnO,设BnCn与PQ交于点F,则有BnO2=OF2+BnF2,
即1=(nh-1)2+![]() .
.
∵h=![]() an,∴1=
an,∴1=![]() an2+
an2+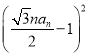 ,
,
解得an=![]() .
.


科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
在“平行四边形、菱形、矩形、正方形”中是“等邻边四边形”的是 .
(2)概念应用
在Rt△ABC中,∠C=![]() ,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .
,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某校在慈善爱心捐款活动中的统计情况,图1是各年级捐款人数占总捐款人数的百分比,图2是对部分学生捐款金额和人数的抽样调查.
(1)在抽取的样本中,捐款金额的平均数、中位数、众数各是多少?
(2)若该校九年级共有200人捐款,请你估计全校捐款的总金额约为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
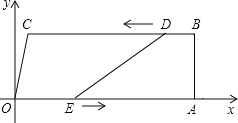
【题目】如图,在四边形OABC中,OA∥BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个,设甲每天加工x个A型零件.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为30元/件,加工一个B型零件所获得的利润每件比A型少5元.现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于8250元,求至少应生产多少个A型零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用同样大小的黑色棋子按如图所示的规律摆放,第1个图形有6颗棋子,第2个图形有9颗棋子,第3个图形有12颗棋子,第4个图形有15颗棋子……,以此类推,第( )个图形有2019颗棋子.

A.672B.673C.674D.675
查看答案和解析>>
科目:初中数学 来源: 题型:
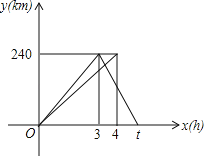
【题目】一辆轿车从甲地驶往乙地,到达乙地后返回甲地,速度是原来的1.5倍,共用t小时;一辆货车同时从甲地驶往乙地,到达乙地后停止.两车同时出发,匀速行驶.设轿车行驶的时间为x(h),两车到甲地的距离为y(km),两车行驶过程中y与x之间的函数图象如图.
(1)求轿车从乙地返回甲地时的速度和t的值;
(2)求轿车从乙地返回甲地时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)直接写出轿车从乙地返回甲地时与货车相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
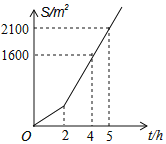
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
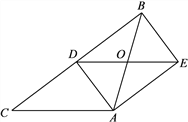
【题目】如图,在△ABC中,AB=AC,AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E.
(1)求证:四边形ADBE是矩形;
(2)连接DE,交AB于点O,若BC=8,AO=![]() ,求cos∠AED的值.
,求cos∠AED的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com