
【题目】某工厂,甲负责加工A型零件,乙负责加工B型零件.已知甲加工60个A型零件所用时间和乙加工80个B型零件所用时间相同,每天甲、乙两人共加工两种零件35个,设甲每天加工x个A型零件.
(1)求甲、乙每天各加工多少个零件;
(2)根据市场预测估计,加工一个A型零件所获得的利润为30元/件,加工一个B型零件所获得的利润每件比A型少5元.现在需要加工甲、乙两种零件共300个且要求所获得的总利润不低于8250元,求至少应生产多少个A型零件?
【答案】(1)甲每天加工15个,乙每天加工20个;(2)至少应生产150个A型零件.
【解析】试题分析:(1)根据题意可得![]() ,解可得x的值,进而可得答案;
,解可得x的值,进而可得答案;
(2)设应生产a个A型零件,依据“需要加工甲、乙两种零件共300个且要求所获得的总利润不低于8250元”列出不等式并解答.
试题解析:
(1)根据题意,每天甲、乙两人共加工35个零件,
设甲每天加工x个,则乙每天加工35﹣x;根据题意可得:
![]() ,
,
解得x=15,
经检验,x=15是原方程的解,且符合题意.
35﹣15=20,
答:甲每天加工15个,乙每天加工20个;
(2)设应生产a个A型零件,则需要加工(300﹣a)个B型零件,
依题意得:30a+(300﹣a)(30﹣5)≥8250,
解得a≥150.
所以a最小值为150.
答:至少应生产150个A型零件.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划购进A,B两个品种的果树苗栽植培育.若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.求y与x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为![]() ,宽为b
,宽为b![]() 的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
的小长方形纸片,按如图2、3的方式不重叠地放在 矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.
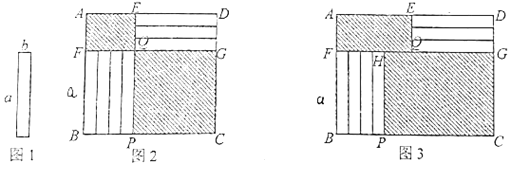
(1)如图2,点E、Q、P在同一直线上,点F、Q、G在同一直线上,右下角与左上角的阴影部分的面积的差为____________(用含![]() 、
、![]() 的代数式表示),矩形ABCD的面积为____________(用含
的代数式表示),矩形ABCD的面积为____________(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(2)如图3,点F、H、Q、G在同一直线上,设右下角与左上角的阴影部分的面积的差为S,![]() .
.
①用![]() 、
、![]() 、
、![]() 的代数式表示AE;
的代数式表示AE;
②当BC的长度变化时,按照同样的放置方式,S始终保持不变,那么![]() 、
、![]() 必须满足什么条件?
必须满足什么条件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF,
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某巡警车在一条南北大道上巡逻,某天巡警车从岗亭![]() 处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
处出发,规定向北方向为正,当天行驶纪录如下(单位:千米)
﹣10,﹣9,+7,﹣15,+6,﹣5,+4,﹣2
![]()
(1)最终巡警车是否回到岗亭![]() 处?若没有,在岗亭何方,距岗亭多远?
处?若没有,在岗亭何方,距岗亭多远?
(2)摩托车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,如图所示.
,如图所示.
![]()
(1)将点![]() 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________;
(2)将点![]() 向左平移3个单位得到数
向左平移3个单位得到数![]() ,再向右平移2个单位得到数
,再向右平移2个单位得到数![]() ,则
,则![]() ,
,![]() 分别是多少?
分别是多少?
(3)怎样移动![]() 、
、![]() 、
、![]() 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五·一”假期的某天,小明、小东两人同时分别从家出发骑共享单车到奥林匹克公园,已知小明家到公园的路程为15km,小东家到公园的路程为12km,小明骑车的平均速度比小东快3.5km/h,结果两人同时到达公园.求小东从家骑车到公园的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com