
【题目】类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.
(1)概念理解
在“平行四边形、菱形、矩形、正方形”中是“等邻边四边形”的是 .
(2)概念应用
在Rt△ABC中,∠C=![]() ,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .
,AB=5,AC=3.点D是AB边的中点,点E是BC边上的一个动点,若四边形ADEC是“等邻边四边形”,则CE= .

 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,
(1)若半径为1的⊙O经过点A、B、D,且∠A=60°,求此时菱形的边长;
(2)若点P为AB上一点,把菱形ABCD沿过点P的直线a折叠,使点D落在BC边上,利用无刻度的直尺和圆规作出直线a.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:有边长为a的正方形A类卡片、边长为b的正方形B类卡片、长和宽分别为a、b的长方形C类卡片各若干张,如果要拼一个边长分别为![]() 、
、![]() 的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )
的大长方形(不重叠无缝隙),那么需要A类卡片______张,B类卡片_______张,C类卡片______张,并请画出一种拼法.(每类卡片至少使用一张,并在画图时标注好每类卡片的类型及边长 )

查看答案和解析>>
科目:初中数学 来源: 题型:
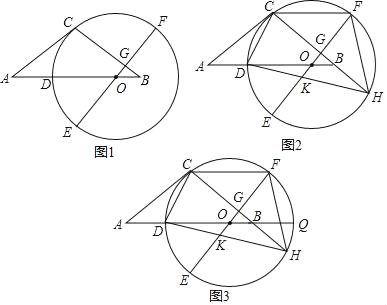
【题目】如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆与AC相切于点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G.
(1)求证:D是弧EC的中点;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点K,连接CF,求证:CF=OK+DO;
(3)如图3,在(2)的条件下,延长DB交⊙O于点Q,连接QH,若DO=![]() ,KG=2,求QH.
,KG=2,求QH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新果树品种,某果园计划购进A,B两个品种的果树苗栽植培育.若计划购进这两种果树苗共45棵,其中A种树苗的单价为7元/棵,购买B种树苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.求y与x的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴和y轴上,OA=1,OB=![]() ,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。
,连接AB,过AB中点C1分别作x轴和y轴的垂线,垂足分别是点A1、B1,连接A1B1,再过A1B1中点C2作x轴和y轴的垂线,照此规律依次作下去,则点Cn的坐标为 ___________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,其中点B的坐标为(1,0),若抛物线y=x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少? .
(2)请用两种不同的方法求图乙中阴影部分的面积.
方法一: ;方法二: .
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2;(m﹣n)2; mm
(4)根据(3)题中的等量关系,解决如下问题:若a+b=8,ab=5,求(a﹣b)2的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知⊙O的半径为1,PQ是⊙O的直径,n个相同的正三角形沿PQ排成一列,所有正三角形都关于PQ对称,其中第一个△A1B1C1的顶点A1与点P重合,第二个△A2B2C2的顶点A2是B1C1与PQ的交点……最后一个△AnBnCn的顶点Bn,Cn在圆上.



(1)如图②,当n=1时,求正三角形的边长a1.
(2)如图③,当n=2时,求正三角形的边长a2.
(3)如图①,求正三角形的边长an(用含n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com