
【题目】如图,四边形ABCD是正方形,点P,Q分别在边AB,BC的延长线上且BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②△OAE∽△OPA;③当正方形的边长为3,BP=1时,cos∠DFO=![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )
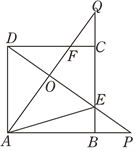
A. 0 B. 1 C. 2 D. 3
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(感知)如图①,![]() ,点
,点![]() 在直线
在直线![]() 与
与![]() 之间,连接
之间,连接![]() 、
、![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
.下面给出了这道题的解题过程,请完成下面的解题过程(填恰当的理由).
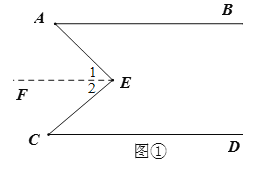
证明:如图①过点![]() 作
作![]() .
.
![]() ( ),
( ),
![]() (已知),EF
(已知),EF![]() (辅助线作法),
(辅助线作法),
![]() ( ),
( ),
![]() ( ),
( ),
![]() ,
,
![]() ( ).
( ).
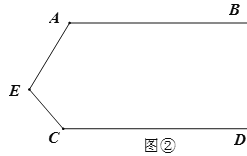
(2)(探究)当点![]() 在如图②的位置时,其他条件不变,试说明
在如图②的位置时,其他条件不变,试说明![]() .
.
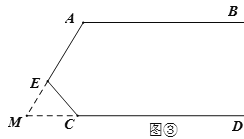
(3)(应用)如图③,延长线段![]() 交直线
交直线![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 的度数为 .(请直接写出答案)
的度数为 .(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明和爸爸在400米的环形跑道上骑车锻炼,他们在同一地点沿着同一方向同时出发,骑行结束后两人有如下对话:

(1)他们的对话内容,求小明和爸爸的骑行速度,
(2)一次追上小明后,在第二次相遇前,再经过多少分钟,小明和爸爸相距50m?
查看答案和解析>>
科目:初中数学 来源: 题型:
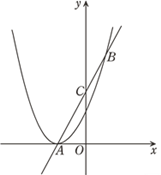
【题目】如图,抛物线y1=ax2+2ax+1与![]() 轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
轴有且仅有一个公共点A,经过点A的直线y2=kx+b交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.
(1)求![]() 的值;
的值;
(2)求直线AB对应的函数解析式;
(3)直接写出当y1 ≥y2 时,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,AC=3,∠ABC=30°.
(1)尺规作图:求作△ABC的外接圆,保留作图痕迹,不写作法;
(2)求(1)中所求作的圆的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
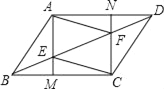
【题目】如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c,ab<0,ac>0,且|c|>|b|>|a|,数轴上a,b,c对应的点分别为A,B,C.
(1)若a=1,请你在数轴上标出点A,B,C的大致位置;
(2)若|a|=﹣a,则a 0,b 0,c 0;(填“>”、“<“或“=”)
(3)小明判断|a﹣b|﹣|b+c|+|c﹣a|的值一定是正数,小明的判断是否正确?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
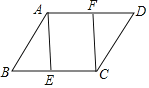
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件:如图所示,在四边形ABCD中,点E、F分别在边BC、AD上,____,求证:四边形AECF是平行四边形. 你能在横线上填上最少且简捷的条件使结论成立吗?
条件分别是:①BE=DF;②∠B=∠D;③BAE=∠DCF;④四边形ABCD是平行四边形.
其中A、B、C、D四位同学所填条件符合题目要求的是( )
A. ①②③④B. ①②③C. ①④D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com