
【题目】如图,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,线段
两点,线段![]() 上有一动点
上有一动点![]() 由原点
由原点![]() 向点
向点![]() 运动,速度为每秒
运动,速度为每秒![]() 个单位长度,设运动时间为
个单位长度,设运动时间为![]() 秒.
秒.

![]() 直接填出两点的坐标:
直接填出两点的坐标:![]() :________,
:________,![]() :________;
:________;
![]() 过点
过点![]() 作直线截
作直线截![]() ,使截得的三角形与
,使截得的三角形与![]() 相似,若当
相似,若当![]() 在某一位置时,满足条件的直线共有
在某一位置时,满足条件的直线共有![]() 条,
条,![]() 的取值范围是________;
的取值范围是________;
![]() 如图,过点
如图,过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,设以
,设以![]() 为顶点的抛物线
为顶点的抛物线![]() 与直线
与直线![]() 的另一交点为
的另一交点为![]() .
.
①用含![]() 的代数式分别表示
的代数式分别表示![]() ________,
________,![]() ________;
________;
②随着点![]() 运动,
运动,![]() 的长是否为定值?若是,请求出
的长是否为定值?若是,请求出![]() 长;若不是,说明理由;
长;若不是,说明理由;
③设![]() 的
的![]() 边上的高为
边上的高为![]() ,请直接写出当
,请直接写出当![]() 为何值时,
为何值时,![]() 的值最大?
的值最大?

【答案】(1)(4,0),(0,3);(2)0<t≤![]() ;(3)①﹣t,﹣
;(3)①﹣t,﹣![]() t+3;②CD的长为定值,且CD=
t+3;②CD的长为定值,且CD=![]() ;③当t=
;③当t=![]() 时,h的值最大.
时,h的值最大.
【解析】
(1)在直线AB的解析式中,令x=0,能得到点B的坐标;令y=0,能得到点A的坐标.
(2)此题需要注意的是“满足条件的直线共有4条”这个条件,这四条直线中,“过P与直线AB平行的直线、过P与y轴平行的直线、过P与直线AB垂直的直线”这三条直线,点P只要在线段OA上就都能满足“截得的三角形与△ABO相似”,所以求t的取值范围,关键要看第四条,即:当∠PBO=∠BAO时,△PBO、△BAO相似,那么此时点P的位置就能确定符合条件的t的最大值,可根据这个思路解答.
(3)①根据直线AB的解析式,用t表示出点C的坐标,而点C是抛物线的顶点,且抛物线的解析式已表示为顶点式,则m、n的值可求;
②联立直线AB与抛物线的解析式,先求出C、D点的坐标,再判断线段CD的长是否为定值;
③由②的结论知CD是定长,那么以CD为底、点O到直线AB的距离为高即可判断出△OCD的面积是一个定值,反过来看,若以OC为底、h为高,那么当OC最短时,h的值最大;在Rt△AOB中,显然只有当OC⊥AB时,OC最大,此时,先由△AOB的面积求出OC的长,然后在Rt△OCA中,由射影定理求出OP的长,则t值可求.
(1)直线y=﹣![]() x+3中,当x=0时,y=3,即 B(0,3);
x+3中,当x=0时,y=3,即 B(0,3);
当y=0时,x=4,即 A(4,0);
∴A(4,0)、B(0,3).
(2)如图,过P作l∥AB、l⊥OA、l⊥AB时,△PBO、△BAO都相似,此时点P在线段OA上时,都符合要求,所以只考虑第四种情况:
当∠PBO=∠BAO时,Rt△PBO∽Rt△BAO;
易知:tan∠PBO=tan∠BAO=![]() =
=![]() ;
;
在Rt△OBP中,OB=3,则 OP=OBtan∠PBO=3×![]() =/span>
=/span>![]()
∴满足条件的t的取值范围是 0<t≤![]() .
.
(3)①由题意,知:P(t,0),则 C(t,﹣![]() t+3),而抛物线的顶点坐标为 (﹣m,n),∴m=﹣t,n=﹣
t+3),而抛物线的顶点坐标为 (﹣m,n),∴m=﹣t,n=﹣![]() t+3;
t+3;
②由①知:y=(x﹣t)2﹣![]() t+3,联立直线AB的解析式,有:
t+3,联立直线AB的解析式,有:
 ,解得
,解得 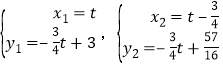 ,∴点C(t,﹣
,∴点C(t,﹣![]() t+3)、D(t﹣
t+3)、D(t﹣![]() ,﹣
,﹣![]() t+
t+![]() );
);
可求得:CD的长为定值,且CD=![]() ;
;
③由②知:CD的长是定值,且点O到CD的距离不变,所以△OCD的面积是定值;
在△OCD中,以OC为底、h为高,则 S△OCD=![]() OCh,S△OCD是定值,所以当OC最短时,h最大;
OCh,S△OCD是定值,所以当OC最短时,h最大;
在Rt△OAB中,OC为底边AB上的高时,OC最短,此时OC⊥AB;
OC=![]() =
=![]() ;
;
在Rt△OAC中,OP=![]() =
=![]() =
=![]() ;
;
∴当t=![]() 时,h
时,h


科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
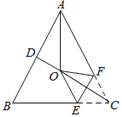
A. 60° B. 55° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从江县盛产椪柑,春节期间,一外地运销客户安排15辆汽车装运A、B、C三种不同品质的椪柑120吨到外地销售,按计划15辆汽车都要装满且每辆汽车只能装同一种品质的椪柑,每种椪柑所用车辆都不少于3辆.
(1)设装运A种椪柑的车辆数为x辆,装运B种椪柑车辆数为y辆,根据下表提供的信息,求出y与x之间的函数关系式;
椪柑品种 | A | B | C |
每辆汽车运载量(吨) | 10 | 8 | 6 |
每吨椪柑获利(元) | 800 | 1200 | 1000 |
(2)在(1)条件下,求出该函数自变量x的取值范围,车辆的安排方案共有几种?请写出每种安排方案;
(3)为了减少椪柑积压,从江县制定出台了促进椪柑销售的优惠政策,在外地运销客户原有获利不变的情况下,政府对外地运销客户,按每吨50元的标准实行运费补贴.若要使该外地运销客户所获利润W(元)最大,应采用哪种车辆安排方案?并求出利润W(元)的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D,且AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )

A. 80° B. 70° C. 60° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,F是CD上一点,E是BF上一点,连接AE、AC、DE.若AB=AC,AD=AE,∠BAC=∠DAE=70°,AE平分∠BAC,则下列结论中:①△ABE≌△ACD:②BE=EF;③∠BFD=110°;④AC垂直平分DE,正确的个数有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,左图为三角形纸片![]() ,点
,点![]() 在
在![]() 上.若将纸片向内折叠,如右图所示,点
上.若将纸片向内折叠,如右图所示,点![]() 、
、![]() 、
、![]() 恰能重合在点
恰能重合在点![]() 处,折痕分别为
处,折痕分别为![]() 、
、![]() 、
、![]() ,折痕的交点
,折痕的交点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上.若
上.若![]() 、四边形
、四边形![]() 的面积分别是20和7,则
的面积分别是20和7,则![]() 的面积是______.
的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(Ⅰ)已知点A与点B关于直线l成轴对称,请尺规作图作出直线l(保留作图痕迹);
(Ⅱ)如图,△ABC(∠B>∠A).

(ⅰ)在边AC上用尺规作图作出点D,使∠ADB+2∠A=180°(保留作图痕迹);
(ⅱ)在(ⅰ)的情况下,连接BD,若CB=CD,∠A=35°,则∠C= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com