Question

【题目】已知，在△ABC中，∠A＝90°，AB＝AC，D为BC的中点，E，F分别是AB，AC上的点，且BE＝AF．

（1）请你判断△DEF形状，并说明理由；

（2）若BE＝2cm，CF＝4cm，求EF的长．

Answer 1

【答案】（1）△DEF是等腰直角三角形，理由详见解析；（2）EF＝2cm．

【解析】

（1）连接AD，构造全等三角形：△BED和△AFD．AD是等腰直角三角形ABC底边上的中线，所以有∠CAD＝∠BAD＝45°，AD＝BD＝CD，而∠B＝∠C＝45°，所以∠B＝∠DAF，再加上BE＝AF，AD＝BD，可证出：△BED≌△AFD，从而得出DE＝DF，∠BDE＝∠ADF，从而得出∠EDF＝90°，即△DEF是等腰直角三角形；

（2）延长ED至G，使得DG＝DE，连接FG，CG，判定△BDE≌△CDG，即可得出CG＝BE＝2cm，∠B＝∠DCG＝45°＝∠ACB，利用勾股定理可得，Rt△CFG中，FG＝＝2cm，再根据FD垂直平分EG，即可得到EF＝GF＝2cm．

解：（1）△DEF是等腰直角三角形．

如图，连接AD，

∵AB＝AC，∠BAC＝90°，D为BC中点，

∴AD＝BC＝BD＝CD，且AD平分∠BAC，

∴∠BAD＝∠CAD＝45°，

在△BDE和△ADF中，

，

∴△BDE≌△ADF（SAS），

∴DE＝DF，∠BDE＝∠ADF，

∵∠BDE+∠ADE＝90°，

∴∠ADF+∠ADE＝90°，即∠EDF＝90°，

∴△EDF为等腰直角三角形．

（2）如图，延长ED至G，使得DG＝DE，连接FG，CG，

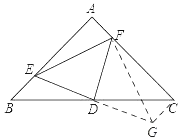
∵D为BC的中点，

∴BD＝CD，

又∵∠BDE＝∠CDG，

∴△BDE≌△CDG，

∴CG＝BE＝2cm，∠B＝∠DCG＝45°＝∠ACB，

∴∠GCF＝90°，

又∵CF＝4cm，

∴Rt△CFG中，FG＝＝＝2cm，

∵∠EDF＝90°，ED＝GD，

∴FD垂直平分EG，

∴EF＝GF＝2cm．