
【题目】某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元时,每天可售出40件,若每件降价10元,则第天多售出10件,请根据以上信息解答下列问题:
(1)为了使销售该品牌衬衫每天获利4500元,并且让利于顾客,每件售价应为多少元;
(2)该服装店将该品牌的衬衫销售完,在补货时厂家只剩100件,经协商每件降价a元,全部拿回。按(1)中的价格售出80件后,剩余的按八折销售。售完这100件衬衫获利20%,求a的值。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
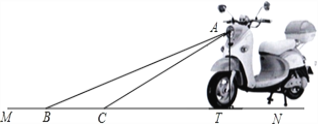
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线![]() 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
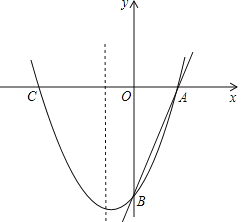
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

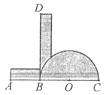

图(1) 图(2) 图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
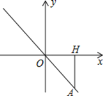
【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com