
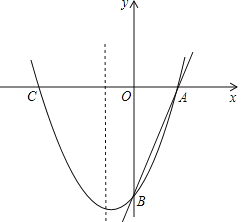
【题目】如图,已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线![]() 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
【答案】(1)![]() ;(2)6;(3)M1(﹣1,
;(2)6;(3)M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() ),M3(﹣1,0),M4(﹣1,﹣1)
),M3(﹣1,0),M4(﹣1,﹣1)
【解析】试题分析:(1)由直线解析式求出点A及点B的坐标,将点A及点B的坐标代入抛物线解析式,可得出b、c的值,即可求出抛物线解析式;
(2)由(1)求得的抛物线解析式,求出点C的坐标,从而求出AC的长度,代入三角形的面积公式即可计算;
(3)根据点M在抛物线对称轴上,可设点M的坐标为(﹣1,m),分三种情况讨论,①MA=BA,②MB=BA,③MB=MA,列方程,求出m的值后即可.
试题解析:(1)∵直线![]() 分别交x轴、y轴于A、B两点,∴可得A(1,0),B(0,﹣3),把A、B两点的坐标分别代入
分别交x轴、y轴于A、B两点,∴可得A(1,0),B(0,﹣3),把A、B两点的坐标分别代入![]() 得:
得:![]() ,解得:
,解得:![]() ,∴抛物线解析式为:
,∴抛物线解析式为:![]() ;
;
(2)令y=0得:![]() ,解得:
,解得:![]() ,
,![]() ,则C点坐标为:(﹣3,0),AC=4,故可得S△ABC=
,则C点坐标为:(﹣3,0),AC=4,故可得S△ABC=![]() AC×OB=
AC×OB=![]() ×4×3=6;
×4×3=6;
(3)存在,理由如下:抛物线的对称轴为:x=﹣1,假设存在M(﹣1,m)满足题意:分三种情况讨论:
①当MA=AB时,∵OA=1,OB=3,∴AB=![]() ,
,![]() ,解得:m=
,解得:m=![]() ,∴M1(﹣1,
,∴M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() );
);
②当MB=BA时,![]() ,解得:M3=0,M4=﹣6,∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去);
,解得:M3=0,M4=﹣6,∴M3(﹣1,0),M4(﹣1,﹣6)(不合题意舍去);
③当MB=MA时,![]() ,解得:m=﹣1,∴M5(﹣1,﹣1),答:共存在4个点M1(﹣1,
,解得:m=﹣1,∴M5(﹣1,﹣1),答:共存在4个点M1(﹣1,![]() ),M2(﹣1,
),M2(﹣1,![]() ),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.
),M3(﹣1,0),M4(﹣1,﹣1)使△ABM为等腰三角形.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.

(1)求证:△ADE≌△CFE;
(2)若GB=2,BC=4,BD=1,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.
![]()
(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是平角,OD是∠AOC的角平分线,∠COE=∠BOE.

(1)若∠AOC= 50°,则∠DOE= °;
(2)当∠AOC的大小发生改变时,∠DOE的大小是否发生改变?为什么?
(3)图中与∠COD互补角的个数随∠AOC的度数变化而变化,直接写出与∠COD互补的角的个数及对应的∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知忠华家、桂枝家、文兴家及学校在一条南北向的大街旁.一天,放学后他们三人从学校出发,先向南走250米达到桂枝家(记为点A),然后再向南走250米到文兴家(记为点B),从文兴家向北走1000米到达忠华家(记为点C).
(1)以学校为原点,以向北方向为正方向,用1个单位长度表示实际距离250米画出一条数轴,在数轴上用字母表示出忠华家、桂枝家、文兴家的位置.
(2)忠华家在学校的哪个方向,到学校的距离是多少米?
(3)如果以向南方向为正方向建立数轴,对确定忠华家相对于学校的位置有影响吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元时,每天可售出40件,若每件降价10元,则第天多售出10件,请根据以上信息解答下列问题:
(1)为了使销售该品牌衬衫每天获利4500元,并且让利于顾客,每件售价应为多少元;
(2)该服装店将该品牌的衬衫销售完,在补货时厂家只剩100件,经协商每件降价a元,全部拿回。按(1)中的价格售出80件后,剩余的按八折销售。售完这100件衬衫获利20%,求a的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮甲从港口O出发,沿东偏南![]() 的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)
的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)

(1)写出在港口O观测灯塔B,C的方向及它们与港口的距离;
(2)已知灯塔D在港口O的南偏西![]() 方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.
方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.
(3)货轮乙从港口O出发,沿正东方向航行15海里到达P处后,需把航行方向调整到与货轮甲的航行方向一致,此时货轮乙应向左(或右)转多少度?并画出货轮乙航行线路示意图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com