
【题目】如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.
![]()
(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值为 .
的值为 .
(3)有一动点Q从原点O出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动到2015次时,求点Q所对应的有理数.
【答案】(1)a=﹣2,b=6;(2)①点P的运动时间t为6或14秒;②2;(3)点Q所对应的有理数的值为﹣1008.
【解析】
试题分析:(1)根据非负数的性质即可求出a、b的值;
(2)①先表示出运动t秒后P点对应的数为﹣2+t,再根据两点间的距离公式得出PO=|﹣2+t|,PB=|﹣2+t﹣6|=|t﹣8|,利用PO=2PB建立方程,求解即可;
②根据中点坐标公式分别表示出点E表示的数,点F表示的数,再计算![]() 即可;
即可;
(3)根据题意得到点P每一次运动后所在的位置,然后由有理数的加法进行计算即可.
解:(1)∵|a+2|+(3a+b)2=0,
∴a+2=0,3a+b=0,
∴a=﹣2,b=6;
(2)①∵若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
∴运动t秒后P点对应的数为﹣2+t,
∵点A表示的数为﹣2,点B表示的数为6,
∴PO=|﹣2+t|,PB=|﹣2+t﹣6|=|t﹣8|,
当PO=2PB时,有|﹣2+t|=2|t﹣8|,
解得t=6或14.
答:点P的运动时间t为6或14秒;
②当点P运动到线段OB上时,
AP中点E表示的数是![]() =
=![]() ,OB的中点F表示的数是3,
,OB的中点F表示的数是3,
所以EF=3﹣![]() =
=![]() ,
,
则![]() =
=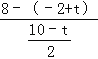 =2;
=2;
(3)依题意得:﹣1+2﹣3+4﹣5+6﹣7+…+2014﹣2015
=(﹣1+2)+(﹣3+4)+(﹣5+6))+…+(﹣2013+2014)﹣2015
=1007﹣2015
=﹣1008.
答:点Q所对应的有理数的值为﹣1008.
故答案为﹣2,6;2.


科目:初中数学 来源: 题型:
【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,点E是BC的中点,F是AB延长线上一点且FB=1.

(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
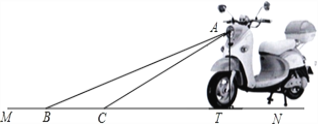
【题目】为响应国家的“节能减排”政策,某厂家开发了一种新型的电动车,如图,它的大灯A射出的光线AB、AC与地面MN的夹角分别为22°和31°,AT⊥MN,垂足为T,大灯照亮地面的宽度BC的长为![]() m.
m.
(1)求BT的长(不考虑其他因素).
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s,从发现危险到电动车完全停下所行驶的距离叫做最小安全距离.某人以20km/h的速度驾驶该车,从做出刹车动作到电动车停止的刹车距离是![]() ,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
,请判断该车大灯的设计是否能满足最小安全距离的要求(大灯与前轮前端间水平距离忽略不计),并说明理由.
(参考数据:sin22°≈![]() ,tan22°≈
,tan22°≈![]() ,sin31°≈
,sin31°≈![]() ,tan31°≈
,tan31°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=3,AB=5,点O在BC边的中线AD上,⊙O与BC相切于点E,且∠OBA=∠OBC.
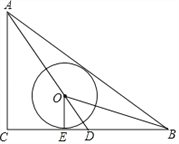
(1)求证:AB为⊙O的切线;
(2)求⊙O的半径;
(3)求tan∠BAD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
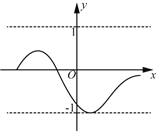
(1)分别判断函数 y=![]() (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数 y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足![]() ≤t≤1?
≤t≤1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级共有500名学生,团委准备调查他们对“低碳”知识的了解程度,
(1)在确定调查方式时,团委设计了以下三种方案:
方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生
请问其中最具有代表性的一个方案是 ;
(2)团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将其补充完整;
(3)请你估计该校七年级约有多少名学生比较了解“低碳”知识.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线![]() 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
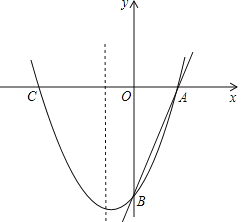
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,D为BC的中点,E,F分别是AB,AC上的点,且BE=AF.
(1)请你判断△DEF形状,并说明理由;
(2)若BE=2cm,CF=4cm,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com