
【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,点E是BC的中点,F是AB延长线上一点且FB=1.

(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)y=-2x2+4x(2)(1,2),(1+![]() ,-2)或(1-
,-2)或(1-![]() ,-2)(3)抛物线上存在点Q(
,-2)(3)抛物线上存在点Q(![]() ,
, ![]() )使△AFQ是等腰直角三角形
)使△AFQ是等腰直角三角形
【解析】试题分析:(1)根据点A、点E的坐标,设出二次函数的解析式,待定系数即可;
(2)判断出面积为2时的点的纵坐标,代入函数可求P点的坐标;
(3)根据题意,分三种情况讨论解答.
试题解析:(1)点A的坐标是(2,0),点E的坐标是(1,2).
设抛物线的解析式是y=ax2+bx+c,根据题意,得
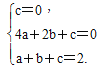
解得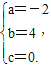
∴抛物线的解析式是y=-2x2+4x.
(2)当△OAP的面积是2时,点P的纵坐标是2或-2.
当-2x2+4x=2时,解得x=1,
∴点P的坐标是(1,2);
当-2x2+4x=-2时,解得x=1±![]() ,
,
此时点P的坐标是(1+![]() ,-2)或(1-
,-2)或(1-![]() ,-2).
,-2).
综上,点P的坐标为(1,2),(1+![]() ,-2)或(1-
,-2)或(1-![]() ,-2).
,-2).
(3)∵AF=AB+BF=2+1=3,OA=2.
则点A是直角顶点时,Q不可能在抛物线上;
当点F是直角顶点时,Q不可能在抛物线上;
当点Q是直角顶点时,Q到AF的距离是![]() AF=
AF=![]() ,若点Q存在,则Q的坐标是(
,若点Q存在,则Q的坐标是(![]() ,
, ![]() ).将Q(
).将Q(![]() ,
, ![]() )代入抛物线解析式成立.
)代入抛物线解析式成立.
∴抛物线上存在点Q(![]() ,
, ![]() )使△AFQ是等腰直角三角形.
)使△AFQ是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】将二次函数y=2x2﹣1的图象向下平移3个单位后所得图象的函数解析式为( )
A.y=2(x﹣3)2﹣1
B.y=2(x+3)2﹣1
C.y=2x2+4
D.y=2x2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现定义某种新运算:对于任意两个有理数a、b,有a*b=a2﹣2b+1,例如:2*3=22﹣2×3+1=﹣1.
(1)计算:3*(﹣2)的值;
(2)试化简:x*(x2+1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,点A是弧BC的中点,AD交BC于E点,AE=2,ED=4. 
(1)求证: ![]() ~△ADB;
~△ADB;
(2) 求![]() 的值;
的值;
(3)延长BC至F,连接FD,使![]() 的面积等于
的面积等于![]() ,求证:DF与⊙O相切。
,求证:DF与⊙O相切。
查看答案和解析>>
科目:初中数学 来源: 题型:
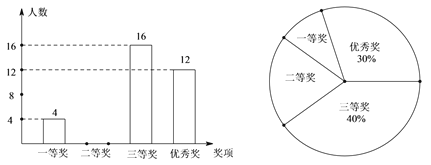
【题目】某中学在全校学生中开展了“地球—我们的家园”为主题的环保征文比赛,评选出一、二、三等奖和优秀奖。根据奖项的情况绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)求校获奖的总人数,并把条形统计图补充完整;
(2)求在扇形统计图中表示“二等奖” 的扇形的圆心角的度数;
(3)获得一等奖的4名学生中有3男1女,现打算从中随机选出2名学生参加颁奖活动,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
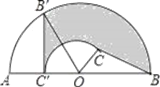
【题目】如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为______cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1 400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需__________元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本);
(3)李大爷现在资金25 000元,他准备再向银行贷不超过25 000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35 000元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com