
����Ŀ����֪�һ��ҡ���֦�ҡ����˼Ҽ�ѧУ��һ���ϱ���Ĵ���ԣ�һ�죬��ѧ���������˴�ѧУ��������������250�״ﵽ��֦�ң���Ϊ��A����Ȼ����������250�����˼ң���Ϊ��B���������˼�����1000�����һ��ң���Ϊ��C����
��1����ѧУΪԭ�㣬������Ϊ��������1����λ���ȱ�ʾʵ�ʾ���250����һ�����ᣬ������������ĸ��ʾ���һ��ҡ���֦�ҡ����˼ҵ�λ�ã�
��2���һ�����ѧУ���ĸ�����ѧУ�ľ����Ƕ����ף�
��3����������Ϸ���Ϊ�����������ᣬ��ȷ���һ��������ѧУ��λ����Ӱ����˵�����ɣ�
���𰸡���1������������2���һ�����ѧУ�ı��棬��ѧУ�ľ�����500�ף���3����������Ϸ���Ϊ�����������ᣬȷ���һ��������ѧУ��λ��û��Ӱ�죬�����������
��������
��1���������⣬ȷ��ԭ�㡢������͵�λ���ȣ���������ȷ����֦�����ˡ��һ��ҵ�λ�ã�
��2�����ݣ�1�������ᣬ�ó��һ�����ѧУ��λ�ú;��룻
��3�����»����ᣬ�ó��һ�����ѧУ��λ�ú;��룮
��1����ΪѧУ��ԭ�㣬����Ϊ��������1����λ���ȱ�ʾ250�ף�
��ѧУ��������250�����֦�ң����Ե�A�ک�1������A������250�������˼ң����Ե�B�ک�2������B����1000���һ��ң����Ե�C��2����
![]()
��2����C��2�������һ�����ѧУ�ı��棬��ѧУ�ľ�����500�ף�
��3����������Ϸ���Ϊ�����������ᣬȷ���һ��������ѧУ��λ��û��Ӱ�죬
��������Ϸ���Ϊ�����������ᣬ�������£�
![]()
��C�ǩ�2�������һ�����ѧУ�ı��棬��ѧУ�ľ�����500�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˽��б�����·����ʱ��Ĺ�ϵ��ͼ��ʾ��
(1)����һ��________�ױ�����
(2)ǰһ��������________���ٶȽϿ죬����________Ӯ���˱�����
(3)���˵�________����;������������ʱ���յ�________�ף�
(4)����ǰ8���ƽ���ٶ��Ƕ��٣������������̵�ƽ���ٶ��Ƕ��٣�����ǰ8���ƽ���ٶ��Ƕ��٣������������̵�ƽ���ٶ��Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ijһ�������������¶��壺������ʵ��M��0����������ĺ���ֵy����������M��y��M���������������н纯��������������������M�У�����Сֵ��Ϊ��������ı߽�ֵ�����磬��ͼ�еĺ������н纯������߽�ֵ��1��
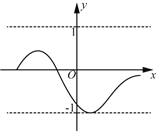
��1���ֱ��жϺ��� y=![]() ��x��0����y=x+1����4��x��2���Dz����н纯���������н纯��������߽�ֵ��
��x��0����y=x+1����4��x��2���Dz����н纯���������н纯��������߽�ֵ��
��2��������y=��x+1��a��x��b��b��a���ı߽�ֵ��2����������������ֵҲ��2����b��ȡֵ��Χ��
��3�������� y=x2����1��x��m��m��0����ͼ������ƽ��m����λ���õ��ĺ����ı߽�ֵ��t����m��ʲô��Χʱ������![]() ��t��1��
��t��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��![]() �ֱ�x�ᡢy����A��B���㣬������
�ֱ�x�ᡢy����A��B���㣬������![]() ����A��B���㣬��C����������x�����һ�����㣨��A�㲻�غϣ���
����A��B���㣬��C����������x�����һ�����㣨��A�㲻�غϣ���
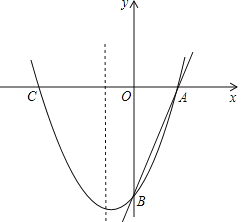
��1���������ߵĽ���ʽ��
��2������ABC�������
��3���������ߵĶԳ����ϣ��Ƿ���ڵ�M��ʹ��ABMΪ���������Σ��������ڣ���˵�����ɣ������ڣ������M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������±����ش����⣺
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
��2x��5 | �� | 9 | 7 | 5 | 3 | a | �� |
2x��8 | �� | 4 | 6 | 8 | 10 | b | �� |
��������֪��
��1��a�� ��b�� ��
�����ɹ��ɣ�
��2������xֵ�ı仯����������ʽ��ֵ�仯������ʲô?
����������
��3���Ƚϣ�2x��5��2x��8�Ĵ�С��
��4����д��һ����x�Ĵ���ʽ��Ҫ��x��ֵÿ����1������ʽ��ֵ��С5����x��0ʱ��
����ʽ��ֵΪ��7.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪OPƽ�֡�AOB����AOB=60�㣬CP=2��CP��OA��PD��OA�ڵ�D��PE��OB�ڵ�E�������M��OP���е㣬��DM�ij��ǣ�������

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��1����Rt��ABC�У���ACB=900,��B=600����ͼ��������ACB�����ȷ���CD,CE.��Ҫ�߹���ͼ�������ۼ�������������
(2)�ɣ�1��֪�����ǿ����ó߹�����ֱ�ǵ����ȷ��ߣ����ǽ���ʹ�ó߹�ȴ���ܰ�����һ���Ƿֳ����ȷ֣�Ϊ�ˣ����Ƿ���������ȷֽǵĻ�е���ߣ���ͼ��2����������ӲֽƬ���Ƶ�һ��������ֽ��������ԲO��ӵ�AB���ij������Բ�İ뾶��ȣ�BD���ij������⣬����һ����ֱ��AC�γ�һ��ֱ�ǣ���־��Բ�����ڵ�B��������Ҫ����KSM���ȷ֣���ͼ��3�������Ƚ��ǵĶ���S����BD�ϣ��ǵ�һ��SK������A����һ��SM���Բ���У�����SO����SB,SOΪ��KSM�����ȷ��ߣ�����֤����

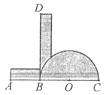

ͼ��1�� ͼ��2�� ͼ��3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=kx��ͼ����A����A�ڵ������ޣ�����A��AH��x�ᣬ����Ϊ��H����A�ĺ�����Ϊ3������AOH�����Ϊ4.5��
��1����������������Ľ���ʽ��
��2����x�����Ƿ����һ��P��ʹ��AOP�����Ϊ6�������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
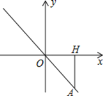
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy����������C��y=mx2+4x+1��
��1����������C������A��-5��6��ʱ���������ߵı���ʽ������������
��2����ֱ��y=-x+l��ֱ��y=x+3����������C�ĶԳ���Գ�ʱ����m��ֵ��
��3����������C��y=mx2+4x+l��m��0����x��Ľ���ĺ����궼��-l��0֮����������-l��0������Ϻ�����ͼ������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com