
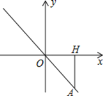
【题目】如图,正比例函数y=kx的图像经过点A,点A在第四象限.过点A做AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为4.5.
(1)求该正比例函数的解析式;
(2)在x轴上是否存在一点P,使△AOP的面积为6?若存在,求点P的坐标;若不存在,请说明理由.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某花店准备购进甲、乙两种花卉,若购进甲种花卉20盆,乙种花卉50盆,需要720元;若购进甲种花卉40盆,乙种花卉30盆,需要880元.
(1)求购进甲、乙两种花卉,每盆各需多少元?
(2)该花店销售甲种花卉每盆可获利6元,销售乙种花卉每盆可获利1元,现该花店准备拿出800元全部用来购进这两种花卉,设购进甲种花卉x盆,全部销售后获得的利润为W元,求W与x之间的函数关系式;
(3)在(2)的条件下,考虑到顾客需求,要求购进乙种花卉的数量不少于甲种花卉数量的6倍,且不超过甲种花卉数量的8倍,那么该花店共有几种购进方案?在所有的购进方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知忠华家、桂枝家、文兴家及学校在一条南北向的大街旁.一天,放学后他们三人从学校出发,先向南走250米达到桂枝家(记为点A),然后再向南走250米到文兴家(记为点B),从文兴家向北走1000米到达忠华家(记为点C).
(1)以学校为原点,以向北方向为正方向,用1个单位长度表示实际距离250米画出一条数轴,在数轴上用字母表示出忠华家、桂枝家、文兴家的位置.
(2)忠华家在学校的哪个方向,到学校的距离是多少米?
(3)如果以向南方向为正方向建立数轴,对确定忠华家相对于学校的位置有影响吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店专营一批进价为每件200元的品牌衬衫,每件售价为300元时,每天可售出40件,若每件降价10元,则第天多售出10件,请根据以上信息解答下列问题:
(1)为了使销售该品牌衬衫每天获利4500元,并且让利于顾客,每件售价应为多少元;
(2)该服装店将该品牌的衬衫销售完,在补货时厂家只剩100件,经协商每件降价a元,全部拿回。按(1)中的价格售出80件后,剩余的按八折销售。售完这100件衬衫获利20%,求a的值。

查看答案和解析>>
科目:初中数学 来源: 题型:
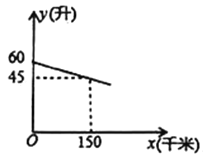
【题目】一辆汽车在某次行驶过程中,油箱中的剩余油量![]() (升)与行驶路程
(升)与行驶路程![]() (千米)之间是一次函数关系,其部分图象如图所示.
(千米)之间是一次函数关系,其部分图象如图所示.
(1)求![]() 关于
关于![]() 的函数关系式;(不需要写自变量
的函数关系式;(不需要写自变量![]() 的取值范围)
的取值范围)
(2)已知当油箱中的剩余油量为10升时,该汽车会开始提示加油,在此次行驶过程中,行驶了482千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】表示有理数a、b的点在数轴上位置如图所示,请解答下列各题:
(1)填空
①|a+2|= ;
②|1﹣b|= ;
③﹣|b﹣a|= ;
(2)化简:|2﹣a|﹣|b﹣1|+|a+b|
(3)若|a|=2.4,|b|=![]() ,则a﹣b= .
,则a﹣b= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,货轮甲从港口O出发,沿东偏南![]() 的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)
的方向航行20海里后到达A处.(已知四个圆圈的半径(由小到大)分别是5海里,10海里,15海里,20海里.)

(1)写出在港口O观测灯塔B,C的方向及它们与港口的距离;
(2)已知灯塔D在港口O的南偏西![]() 方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.
方向上,且与灯塔B相距35海里,在图中标出灯塔D的位置.
(3)货轮乙从港口O出发,沿正东方向航行15海里到达P处后,需把航行方向调整到与货轮甲的航行方向一致,此时货轮乙应向左(或右)转多少度?并画出货轮乙航行线路示意图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com