
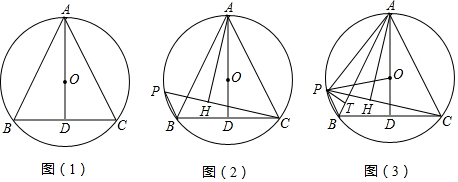
分析 (1)根据垂径定理的推论即即可证明;
(2)如图2中,在CH上取一点E使得HP=HE,连接AP、AE,设PC与AD交于点G.只要证明△PAB≌△EAC,推出PB=EC即可解决问题;
(3)如图3中,作PM⊥CB交CB的延长线于M,OP的延长线交AC于K.设PH=a,CH=b.首先证明PA=PC=a+b,利用勾股定理列出方程组求出a、b,由△PAH∽△BAD,可得$\frac{PA}{AB}$=$\frac{PH}{BD}$,TC BD=$\frac{20\sqrt{13}}{13}$,BC=$\frac{40\sqrt{13}}{13}$由△PAT≌△PCM,可得AT=CM.BM=TB,TC AB+BC=AT+TB+CM-BM=2AT,由此即可解决问题;
解答 (1)证明:如图1中,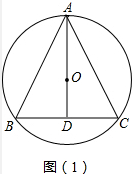
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴OA⊥BC,即AD⊥BC,
∴BD=CD.
(2)证明:如图2中,在CH上取一点E使得HP=HE,连接AP、AE,设PC与AD交于点G.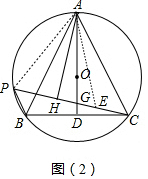
∵AH⊥PE,PH=HE,
∴AP=AE,
∴∠PAH=∠EAH,
∵AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵∠PAH+∠APH=90°,∠ABD+∠BAD=90°,∠APH=∠ABD,
∴∠PAH=∠BAD,
∴∠EAH=∠CAD,
∴∠HAG=∠CAE,
∵∠AHG=∠CDG=90°,∠AGH=∠CGD,
∴∠HAG=∠DCG=∠PAB,
∴∠PAB=∠CAE,∵AP=AE,AB=AC,
∴△PAB≌△EAC,
∴PB=EC,
∴CH=CE+EH=PB+PH.
(3)解:如图3中,作PM⊥CB交CB的延长线于M,OP的延长线交AC于K.设PH=a,CH=b.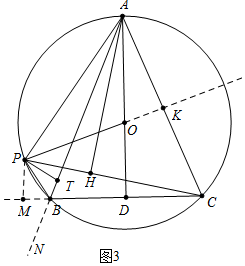
∵PB=3,
∴b=a+3 ①,
∵∠AOP=90°+∠BAD,∠NBD=∠ADB+∠BAD=90°+∠BAD,
∴∠AOP=∠NBD,
∴∠POD=∠ABD=∠ACB,
∵∠POD+∠DOK=180°,
∴∠DOK+∠DCK=180°,
∴∠ODC+∠OKC=180°,∵∠ODC=90°,
∴∠OKC=90°,即PO⊥AC,
∴KA=KC,PA=PC=a+b,
∵AH⊥PC,
∴AH2=PA2-PH2=AC2-HC2,
∴(a+b)2-a2=(4$\sqrt{13}$)2-b2 ②,
由①②可得a=5,b=8,
由△PAH∽△BAD,可得$\frac{PA}{AB}$=$\frac{PH}{BD}$,
∴BD=$\frac{20\sqrt{13}}{13}$,BC=$\frac{40\sqrt{13}}{13}$
由△PAT≌△PCM,可得AT=CM.BM=TB,
∴AB+BC=$\frac{AT}{\;}$AT+TB+CM-BM=2AT=4$\sqrt{13}$+$\frac{40\sqrt{13}}{13}$,
∴AT=$\frac{46\sqrt{13}}{13}$.
点评 本题考查圆综合题、垂径定理以及推论、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、二元二次方程组等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用构建方程组的思想思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
 如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.
如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于8cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
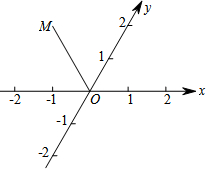 在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )
在平面上,过一定点O作两条斜交的轴x和y,它们的交角是ω(ω≠90°),以定点O为原点,在每条轴上取相同的单位长度,这样就在平面上建立了一个斜角坐标系,其中ω叫做坐标角.对于平面内任意一点P,过P作x轴和y轴的平行线,与两轴分别交于A和B,它们在两轴的坐标分别是x和y,于是点P的坐标就是(x,y).如图,ω=60°,且y轴平分∠MOx,OM=2,则点M的坐标是( )| A. | (2,-2) | B. | (-1,2) | C. | (-2,2) | D. | (-2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
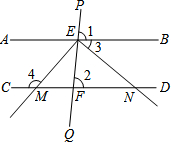 已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.
已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 对角线平分一组对角的四边形是菱形 | |
| D. | 对角线互相垂直的四边形是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com