
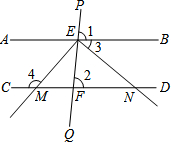
 已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.
已知:如图,直线PQ分别与直线AB、CD交于点E和点F,∠1=∠2,射线EM、EN分别与直线CD交于点M、N,且EM⊥EN,∠3=40°,求∠4的度数.分析 根据平行线的判定得出AB∥CD,根据垂直求出∠MEN=90°,求出∠BEM,根据平行线的性质得出即可.
解答 解:∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行),
∵EM⊥EN,
∴∠MEN=90°(垂直定义),
∵∠3=40°,
∴∠BEM=∠3+∠MEN=40°+90°=130°,
∵AB∥CD,
∴∠4=∠BEM=130°(两直线平行,内错角相等),
故答案为:AB,CD,同位角相等,两直线平行,∠MEN=90°,垂直定义,3,MEN,40,90,130,BEM,两直线平行,内错角相等,130.
点评 本题考查了垂直定义和平行线的性质和判定,能熟练地运用平行线的性质和判定进行推理是解此题的关键.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
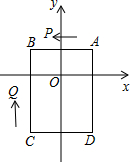 如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).
如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
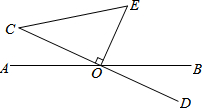 如图,AB,CD交于点O,OE⊥CD于O,连接CE,
如图,AB,CD交于点O,OE⊥CD于O,连接CE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.
如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
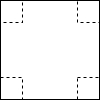 如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.
如图,把一边长为xcm的正方形纸板的四个角各剪去一个边长为ycm的小正方形,然后把它折成一个无盖纸盒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com