
已知凸四边形ABCD中,∠A=∠C=90°.
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明。
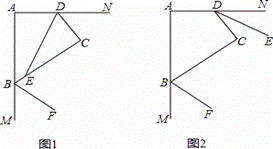
(1)解:延长DE交BF于点G………(1分)
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC…………(2分)
 ∵DE、BF分别平分∠ADC、∠MBC
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=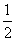 ∠ADC,∠EBG=
∠ADC,∠EBG=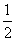 ∠MBC,(3分)
∠MBC,(3分)
∴∠EDC=∠EBG…………(4分)
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG ∴∠EGB=∠C=90
∴ DE⊥BF……………(5分)
(2)解:连接BD…… …………(6分)
…………(6分)
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=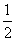 ∠NDC,∠FBC=
∠NDC,∠FBC= ∠MBC,(7分)
∠MBC,(7分)
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC= 90°………………(8分)
90°………………(8分)
∵∠C=90° ∴∠CDB+∠CBD=90°
 ∴∠EDC+∠CDB +∠FBC +∠CBD=180°
∴∠EDC+∠CDB +∠FBC +∠CBD=180°
即∠EDB+∠FBD=180°……………(9分)
∴ D E∥BF……………(10分)
E∥BF……………(10分)


科目:初中数学 来源: 题型:
如图,在在平面直角坐标 系中,四边形ABCD是梯形,AD∥BC,
系中,四边形ABCD是梯形,AD∥BC,
E是BC的中点,BC=12,点A坐标是(0,4),CD所在直线的函数关系式为y= -x+9,
点P是BC边上一个动点,
⑴ 当PB= 时,以点P、A、D、E为顶点的四边形为平行四边形;
⑵ 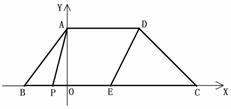 在⑴的条件下,点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否
在⑴的条件下,点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否
构成菱形?试说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
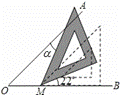
用等腰直角三角板画∠ AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为 度.
AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为 度.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法中,正确的个数有
①一组数据的平均数一定是该组数据中的某个数据;
②一组数据的中位数一定是该组数据中的某个数据;
③一组数据的众数一定是该组数据中的某个数据.
(A)0个; (B)1个; (C)2个; (D)3个.
查看答案和解析>>
科目:初中数学 来源: 题型:
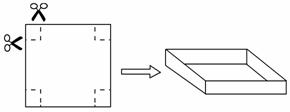
把一张边长为40 cm的正方形硬纸板,进行适当的裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余 部分折成一个无盖的长方体盒子.
部分折成一个无盖的长方体盒子.

①要使折成的长方体盒子的底面积为484 cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为550 cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com