
【题目】如图,直线AB、CD相交于点O,OE把![]() 分成两部分;
分成两部分;
(1)直接写出图中![]() 的对顶角为 ,
的对顶角为 ,![]() 的邻补角为 ;
的邻补角为 ;
(2)若![]() ,且
,且![]() ,求
,求![]() 的度数.
的度数.
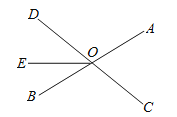
【答案】(1)∠BOC,∠BOE;(2)138°
【解析】分析:(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等和∠AOC:∠DOE=5:3,得到∠BOD:∠DOE=5:3,设∠BOD=5x,则∠DOE=3x,∠BOE=2x.求出x的值,即可得到结论.
详解:(1)∠AOD的对顶角为∠BOC,∠AOE的邻补角为∠BOE;
(2)∵∠AOC=∠BOD,∠AOC:∠DOE=5:3,∴∠BOD:∠DOE=5:3.
设∠BOD=5x,则∠DOE=3x,∴∠BOE=∠BOD-∠DOE=5x-3x=2x .
∵∠BOE=28°,∴2x=28°, ∴x=14°,
∴∠DOE=3x=3×14°=42°.
∵∠DOE+∠COE=180°,
∴∠COE=180°-∠DOE=180°-42°=138°.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】如图,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(﹣1,0),与y轴交于点C(0,4),作直线AC.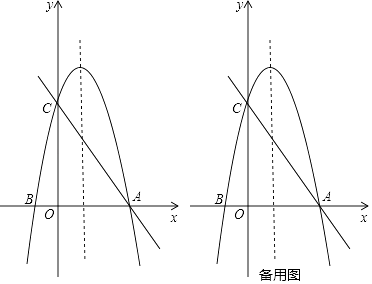
(1)求抛物线解析式;
(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等,设点P的纵坐标为m,求m的值;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C、M、N、Q为顶点的四边形是菱形,请直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学本学年每个单元的测验成绩如下(单位:分):
甲:98,100,100,90,96,91,89,99,100,100,93
乙:98,99,96,94,95,92,92,98,96,99,97
(1)、他们的平均成绩分别是多少?
(2)、甲、乙的11次单元测验成绩的标准差分别是多少?
(3)、这两位同学的成绩各有什么特点?
(4)、现要从中选出一人参加“希望杯”竞赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这项竞赛,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图(1))和条形图(如图(2)),经确认扇形图是正确的,而条形图尚有一处错误. 回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的: 第一步:求平均数的公式是 ![]() =
= ![]() ;
;
第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7;
第三步: ![]() =
= ![]() =5.5(份)
=5.5(份)
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、F分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:
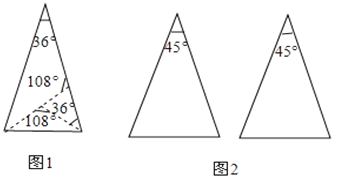
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
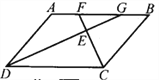
【题目】(本题8分)如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.
(1)试说明AF=GB;
(2)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com