
【题目】如图,以x=1为对称轴的抛物线y=ax2+bx+c的图象与x轴交于点A,点B(﹣1,0),与y轴交于点C(0,4),作直线AC.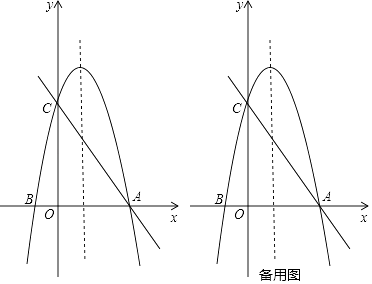
(1)求抛物线解析式;
(2)点P在抛物线的对称轴上,且到直线AC和x轴的距离相等,设点P的纵坐标为m,求m的值;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点Q为第一象限内抛物线上一点,若以点C、M、N、Q为顶点的四边形是菱形,请直接写出点Q的坐标.
【答案】
(1)
解:∵点A与点B(﹣1,0)关于直线x=1对称,
∴A(3,0),
设抛物线解析式为y=a(x+1)(x﹣3),
把C(0,4)代入得a1(﹣3)=4,解得a=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() (x+1)(x﹣3),即y=﹣
(x+1)(x﹣3),即y=﹣ ![]() x2+
x2+ ![]() x+4;
x+4;
(2)
解:设直线AC的解析式为y=kx+p,
把A(3,0),C(0,4)代入得 ![]() ,解得
,解得 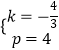 ,
,
∴直线AC的解析式为y=﹣ ![]() x+4;
x+4;
令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,
当x=1时,y=﹣ ![]() x+4=
x+4= ![]() ,则D(1,
,则D(1, ![]() ),
),
∴DE= ![]() ,
,
在Rt△ADE中,AD= ![]() =
= ![]() ,
,
设P(1,m),则PD= ![]() ﹣m,PH=PE=|m|,
﹣m,PH=PE=|m|,
∵∠PDH=∠ADE,
∴△DPH∽△DAE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得m=1或m=﹣4,
,解得m=1或m=﹣4,
即m的值为1或﹣4;
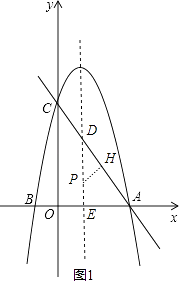
(3)
解:设Q(t,﹣ ![]() t2+
t2+ ![]() t+4)(0<t<4),
t+4)(0<t<4),
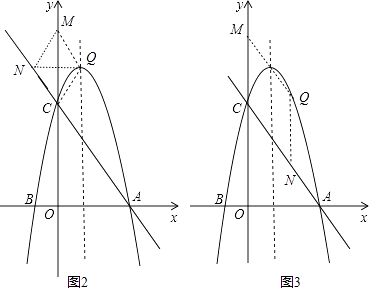
当CM为对角线时,四边形CQMN为菱形,如图2,则点N和Q关于y轴对称,
∴N(﹣t,﹣ ![]() t2+
t2+ ![]() t+4),
t+4),
把N(﹣t,﹣ ![]() t2+ /span>
t2+ /span>![]() t+4)代入y=﹣
t+4)代入y=﹣ ![]() x+4得
x+4得 ![]() t+4=﹣
t+4=﹣ ![]() t2+
t2+ ![]() t+4,解得t1=0(舍去),t2=1,此时Q点坐标为(1,
t+4,解得t1=0(舍去),t2=1,此时Q点坐标为(1, ![]() );
);
当CM为菱形的边时,四边形CNQM为菱形,如图3,则NQ∥y轴,NQ=NC,
∴N(t,﹣ ![]() t+4),
t+4),
∴NQ=﹣ ![]() t2+
t2+ ![]() t+4﹣(﹣
t+4﹣(﹣ ![]() t+4)=﹣
t+4)=﹣ ![]() t2+4t,
t2+4t,
而CN2=t2+(﹣ ![]() t+4﹣4)2=
t+4﹣4)2= ![]() t2,即CN=
t2,即CN= ![]() t,
t,
∴﹣ ![]() t2+4t=
t2+4t= ![]() t,解得t1=0(舍去),t2=
t,解得t1=0(舍去),t2= ![]() ,此时Q点坐标为(
,此时Q点坐标为( ![]() ,
, ![]() ),
),
综上所述,点Q的坐标为(1, ![]() )或(
)或( ![]() ,
, ![]() ).
).
【解析】(1)先利用抛物线的对称性得到A(3,0),则可设交点式y=a(x+1)(x﹣3),然后把C点坐标代入求出a即可;(2)先利用待定系数法其出直线AC的解析式为y=﹣ ![]() x+4;令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,易得D(1,
x+4;令对称轴与直线AC交于点D,与x轴交于点E,作PH⊥AD于H,如图1,易得D(1, ![]() ),利用勾股定理计算出AD=
),利用勾股定理计算出AD= ![]() ,设P(1,m),则PD=
,设P(1,m),则PD= ![]() ﹣m,PH=PE=|m|,证明△DPH∽△DAE,利用相似比得到
﹣m,PH=PE=|m|,证明△DPH∽△DAE,利用相似比得到 ![]() =
= ![]() ,然后解方程可得到m的值;(3)设Q(t,﹣
,然后解方程可得到m的值;(3)设Q(t,﹣ ![]() t2+
t2+ ![]() t+4)(0<t<4),讨论:当CM为对角线时,四边形CQMN为菱形,如图2,根据菱形的性质判定点N和Q关于y轴对称,则N(﹣t,﹣
t+4)(0<t<4),讨论:当CM为对角线时,四边形CQMN为菱形,如图2,根据菱形的性质判定点N和Q关于y轴对称,则N(﹣t,﹣ ![]() t2+
t2+ ![]() t+4),然后
t+4),然后
把N(﹣t,﹣ ![]() t2+
t2+ ![]() t+4)代入y=﹣
t+4)代入y=﹣ ![]() x+4得t的方程,从而解方程求出t得到此时Q点坐标;当CM为菱形的边时,四边形CNQM为菱形,如图3,利用菱形的性质得NQ∥y轴,NQ=NC,则N(t,﹣
x+4得t的方程,从而解方程求出t得到此时Q点坐标;当CM为菱形的边时,四边形CNQM为菱形,如图3,利用菱形的性质得NQ∥y轴,NQ=NC,则N(t,﹣ ![]() t+4),所以NQ=﹣
t+4),所以NQ=﹣ ![]() t2+4t,再根据两点间的距离公式计算出CN=
t2+4t,再根据两点间的距离公式计算出CN= ![]() t,所以﹣
t,所以﹣ ![]() t2+4t=
t2+4t= ![]() t,从而解方程求出t得到此时Q点坐标.
t,从而解方程求出t得到此时Q点坐标.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某市文化宫学习十九大有关优先发展教育的精神,举办了为某贫困山区小学捐赠书包活动.首次用2000元在商店购进一批学生书包,活动进行后发现书包数量不够,又购进第二批同样的书包,所购数量是第一批数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求文化官第一批购进书包的单价是多少?
(2)商店两批书包每个的进价分别是68元和70元,这两批书包全部售给文化宫后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】

A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点. 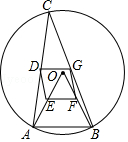
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空: ①若AB=3,当CA=CB时,四边形DEFG的面积是;
②若AB=2,当∠CAB的度数为时,四边形DEFG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.

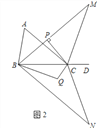
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了拉动内需,全国各地汽车购置税补贴活动正式开始.重庆长安汽车经销商在出台前一个月共售出长安SUV汽车CS35的手动型和自动型共960台,政策出台后的第一月售出这两种型号的汽车共1228台,其中手动型和自动型汽车的销售量分别比政策出台前一个月增长30%和25%.
(1)在政策出台前一个月,销售的手动型和自动型汽车分别为多少台?
(2)若手动型汽车每台价格为8万元,自动型汽车每台价格为9万元.根据汽车补贴政策,政府按每台汽车价格的5%给购买汽车的用户补贴,购车人需要交纳车辆购置各种税费杂费路桥保险等为每台汽车价格的22%,问政策出台后的第一个月,政府对这l228台汽车用户共补贴了多少万元?客户实际需要花多少钱才能够买一辆自动型的CS35汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:(用简便方法计算)
(1)-102n×100×(-10)2n-1; (2)[(-a)(-b)2a2b3c]2;
(3)(x3)2÷x2÷x+x3÷(-x)2(-x2); (4)(-9)3×( -![]() )3
)3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com