
【题目】(本题8分)如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于点F,∠ADC的平分线DG交边AB于点G.
(1)试说明AF=GB;
(2)请你在已知条件的基础上再添加一个条件,使得△EFG为等腰直角三角形,并说明理由.
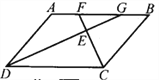
【答案】(1)由角平分线知∠ADG=∠CDG,由平行知∠CDG=∠AGD所以,∠ADG=∠AGD,即AD=AG,同理BF=BC,又AD=BC,所以AG=BF,去掉公共部分,则有AF=GB;(2)EF=EG
【解析】试题分析:(1)由角平分线知∠ADG=∠CDG,由平行知∠CDG=∠AGD所以,∠ADG=∠AGD,即AD=AG,同理BF=BC,又AD=BC,所以AG=BF,去掉公共部分,则有AF=GB;
(2)由于DG、CF是平行四边形一组邻角的平分线,所以△EFG已经是直角三角形了,要成为等腰直角三角形,则必须有EF=EG或者∠EFG=∠EGF即可.
(1)∵四边形ABCD为平行四边形
∴AB∥CD,AD∥BC,AD=BC,
∴∠AGD=∠CDG,∠DCF=∠BFC.
∵DG、CF分别平分∠ADC和∠BCD,
∴∠CDG=∠ADG,∠DCF=∠BCF.
∴∠ADG=∠AGD,∠BFC=∠BCF.
∴AD=AG,BF=BC.
∴AG=BF,即AG-FG=BF-FG
∴AF=BG;
(2)∵AD∥BC
∴∠ADC+∠BCD=180°.
∵DG、CF分别平分∠ADC和∠BCD,
∴∠EDC+∠ECD=90°.
∴∠DEC=90°.
∴∠FEG=90°.
因此我们只要保证添加的条件使得EF=EG就可以了。
我们也可以添加∠GFE=∠FGD,四边形ABCD为矩形,DG=CF等等.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】计算下列各题:(用简便方法计算)
(1)-102n×100×(-10)2n-1; (2)[(-a)(-b)2a2b3c]2;
(3)(x3)2÷x2÷x+x3÷(-x)2(-x2); (4)(-9)3×( -![]() )3
)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一直径是 ![]() 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则: 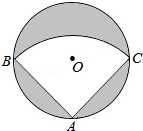
(1)AB的长为米;
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,点C,D在线段AB上,且AC=DB=2;点P是线段CD上的动点,分别以AP,PB为边在线段AB的同侧作等边三角形AEP和等边三角形PFB,连接EF,设EF的中点为G;当点P从点C运动到点D时,点G移动路径的长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表,阅读并回答问题:
抛掷结果 | 10次 | 50次 | 500次 | 5000次 |
出现正面次数 | 3 | 24 | 258 | 2498 |
出现正面的频率 | 30% | 48% | 51.6% | 49.96% |
(1)从表中可知,当抛完10次时正面出现3次,正面出现的频率为30%,那么,小明抛完10次时,得到 次反面,反面出现的频率是 ;
(2)当他抛完5000次时,反面出现的次数是 ,反面出现的频率是 ;
(3)通过上表我们可以知道,正面出现的频数和反面出现的频数之和等于
,正面出现的频率和反面出现的频率之和等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
“若![]() 满足
满足![]() ,求
,求![]() 的值”
的值”
解:设![]() ,则
,则![]() ,
,
所以![]()
(解决问题)
(1)若![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(2)若![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(3)如图,正方形![]() 的边长为
的边长为![]() ,
,![]() ,长方形
,长方形![]() 的面积是500,四边形
的面积是500,四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).
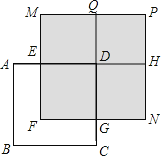
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com