
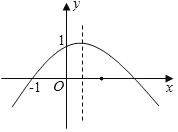
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0),下列结论:①ab<0,②0<b<1,③0<a+b+c<2,④当x>﹣1时,y>0.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
抛物线开口方向得a<0,利用对称轴在y轴的右侧得b>0,则可对①进行判断;根据二次函数图象上点的坐标特征得c=1,a﹣b+c=0,则b=a+c=a+1,所以0<b<1,于是可对②进行判断;由于a+b+c=a+a+1+1=2a+2,利用a<0可得a+b+c<2,再根据抛物线的对称性得到抛物线与x轴的另一个交点在(1,0)和(2,0)之间,则x=1时,函数值为正数,即a+b+c>0,由此可对③进行判断;观察函数图象得到x>﹣1时,抛物线有部分在x轴上方,有部分在x轴下方,则可对④进行判断.
解:∵由抛物线开口向下,
∴a<0,
∵对称轴在y轴的右侧,
∴b>0,
∴ab<0,所以①正确;
∵点(0,1)和(﹣1,0)都在抛物线y=ax2+bx+c上,
∴c=1,a﹣b+c=0,
∴b=a+c=a+1,
而a<0,
∴0<b<1,所以②正确;
∵a+b+c=a+a+1+1=2a+2,
而a<0,
∴2a+2<2,即a+b+c<2,
∵抛物线与x轴的一个交点坐标为(﹣1,0),而抛物线的对称轴在y轴右侧,在直线x=1的左侧,
∴抛物线与x轴的另一个交点在(1,0)和(2,0)之间,
∴x=1时,y>0,即a+b+c>0,
∴0<a+b+c<2,所以③正确;
∵x>﹣1时,抛物线有部分在x轴上方,有部分在x轴下方,
∴y>0或y=0或y<0,所以④错误.
故选C.


科目:初中数学 来源: 题型:
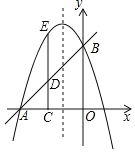
【题目】已知直线y=x+3交x轴于点A,交y轴于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求抛物线解析式;
(2)点C(m,0)在线段OA上(点C不与A,O点重合),CD⊥OA交AB于点D,交抛物线于点E,若DE=![]() AD,求m的值;
AD,求m的值;
(3)点M在抛物线上,点N在抛物线的对称轴上,在(2)的条件下,是否存在以点D,B,M,N为顶点的四边形为平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在研究如何在△ABC内做一个面积最大的正方形时,想到了可以利用位似知识解决这个问题,他的做法是:(如图1)先在△ABC内作一个小正方形DEFG,使得顶点D落在边AB上,顶点E、F落在边BC上,然后连接BG并延长交AC边于点H,作HK⊥BC,HI∥BC,再作IJ⊥BC于J,则正方形HIJK就是所作的面积最大的正方形.
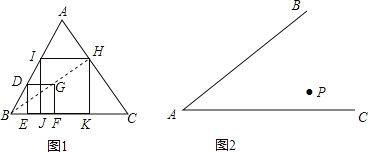
(1)若△ABC中,AB=4,∠ABC=60°,∠ACB=45°,请求出小明所作的面积最大的正方形的边长.
(2)拓展运用:
如图2,已知∠BAC,在角的内部有一点P,请画一个⊙M,使得⊙M经过点P,且与AB、AC都相切.(注:并简要说明画法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的 反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是 “兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某 实验小组做了棋子下掷实验,实验数据如下表:
实验次数 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
“兵”字面朝上频数 | 14 | 38 | 47 | 52 | 66 | 78 | 88 | |
“兵”字面朝上频率 | 0.7 | 0.45 | 0.63 | 0.59 | 0.52 | 0.56 | 0.55 |
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某 一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
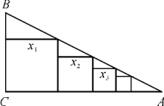
【题目】如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为![]() ,
,![]() ,
,![]() ,…,
,…,![]() 的n
的n![]() 个正方形依次放入△ABC中,则第n个正方形的边长
个正方形依次放入△ABC中,则第n个正方形的边长![]() _______________(用含n的式子表示).
_______________(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
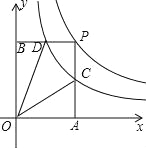
【题目】如图是函数y=![]() 与函数y=
与函数y=![]() 在第一象限内的图象,点P是y=
在第一象限内的图象,点P是y=![]() 的图象上一动点,PA⊥x轴于点A,交y=
的图象上一动点,PA⊥x轴于点A,交y=![]() 的图象于点C,PB⊥y轴于点B,交y=
的图象于点C,PB⊥y轴于点B,交y=![]() 的图象于点D.
的图象于点D.
(1)求证:D是BP的中点;
(2)求四边形ODPC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com