
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
设该二次函数与坐标轴的交点分别为A、B,连接AB,可作直线l∥AB,当直线l与该抛物线只有一个交点时,可设直线l与坐标轴的交点为C、D,求出△OCD的面积即为抛物线图象与两坐标轴所围成的图形最接近的面积.
如图,
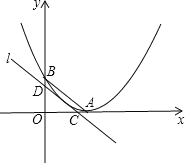
设抛物线与坐标轴的交点为A、B,则有:
A(4,0),B(0,4);
作直线l∥AB,易求得直线AB:y=-x+4,
所以设直线l:y=-x+h,当直线l与抛物线只有一个交点(相切)时,有:
-x+h=![]() (x-4)2,
(x-4)2,
整理得:![]() x2-x+4-h=0,
x2-x+4-h=0,
△=1-4×![]() (4-h)=0,即h=3;
(4-h)=0,即h=3;
所以直线l:y=-x+3;
设直线l与坐标轴的交点为C、D,则C(3,0)、D(0,3),
因抛物线的图象与两坐标轴所围成的图形面积大于S△OCD小于S△OAB
S△OCD=![]() ×3×3=4.5. S△OAB=
×3×3=4.5. S△OAB=![]() ×4×4=8,
×4×4=8,
故抛物线的图象与两坐标轴所围成的图形面积在4.5<S<8的范围内,选项中符合的只有A,
故选A.


科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形的中心在原点![]() ,且正方形的一组对边与
,且正方形的一组对边与![]() 轴平行.点
轴平行.点![]() 是反比例幽数
是反比例幽数![]() 的图象上与正方形的一个交点,若图中阴影部分的面积等于
的图象上与正方形的一个交点,若图中阴影部分的面积等于![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ﹙
﹙![]() ,
,![]() ﹚,
﹚,![]() ﹙
﹙![]() ,
,![]() ﹚,交
﹚,交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .
.

![]() 求反比例函数
求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
![]() 连接
连接![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
![]() 根据图象写出使一次函数的值小于反比例函数的值的
根据图象写出使一次函数的值小于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
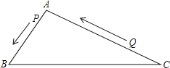
【题目】如图,![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,点
运动,点![]() 从
从![]() 同时出发,以每秒
同时出发,以每秒![]() 厘米的速度向
厘米的速度向![]() 运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以
运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似时,运动时间为________.
相似时,运动时间为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义感知:我们把顶点关于![]() 轴对称,且交于
轴对称,且交于![]() 轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线
轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线![]() 与
与![]() 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点![]() .
.
初步运用:
![]() 判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“
判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“![]() ”:
”:
①“孪生抛物线”的“共点”不能分布在![]() 轴上.________
轴上.________
②“孪生抛物线”![]() 与
与![]() 的“共点”坐标为
的“共点”坐标为![]() .________
.________
![]() 填空:抛物线
填空:抛物线![]() 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为![]() ,
,![]() ,且
,且![]() ,其“共点”
,其“共点”![]() 与
与![]() ,
,![]() ,
,![]() 三点恰好构成一个面积为
三点恰好构成一个面积为![]() 的菱形,试求该“孪生抛物线”的解析式.
的菱形,试求该“孪生抛物线”的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明在一次高尔夫球争霸赛中从山坡上的点![]() 打出一球向球洞
打出一球向球洞![]() 飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度
飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度![]() 时,球移动的水平距离为
时,球移动的水平距离为![]() .已知山坡
.已知山坡![]() 与水平方向
与水平方向![]() 的夹角为
的夹角为![]() ,
,![]() ,
,![]() 两点相距
两点相距![]()
![]() .
.
![]() 求出点
求出点![]() 的坐标;
的坐标;
![]() 求抛物线解析式.并判断小明这一杆能否把高尔夫球从点
求抛物线解析式.并判断小明这一杆能否把高尔夫球从点![]() 直接打入球洞
直接打入球洞![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )
,则在下列条件:①∠C=∠D ②AC=AD ③∠CBA=∠DBA ④BC=BD中任选一个能判定△ABC≌△ABD的是( )

A. ①②③④ B. ②③④ C. ①③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,过点C在△ABC外作直线MN,AM⊥NN于点M,BN⊥MN于N.
(1)求证:△AMC≌△CNB;
(2)求证:MN=AM+BN.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com