
【题目】定义感知:我们把顶点关于![]() 轴对称,且交于
轴对称,且交于![]() 轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线
轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线![]() 与
与![]() 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点![]() .
.
初步运用:
![]() 判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“
判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“![]() ”:
”:
①“孪生抛物线”的“共点”不能分布在![]() 轴上.________
轴上.________
②“孪生抛物线”![]() 与
与![]() 的“共点”坐标为
的“共点”坐标为![]() .________
.________
![]() 填空:抛物线
填空:抛物线![]() 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为![]() ,
,![]() ,且
,且![]() ,其“共点”
,其“共点”![]() 与
与![]() ,
,![]() ,
,![]() 三点恰好构成一个面积为
三点恰好构成一个面积为![]() 的菱形,试求该“孪生抛物线”的解析式.
的菱形,试求该“孪生抛物线”的解析式.

【答案】![]() √
√![]()
【解析】
初步运用:(1)由“孪生抛物线”的意义判断即可,它们的共点在y轴,求出其坐标;
(2)由“孪生抛物线”的顶点关于y轴对称,所以把解析式化成顶点式,求出其“孪生抛物线”;
延伸拓展:由于其“共点”A与M,M′,O三点恰好构成一个面积为12的菱形,且MM′=4,①开口向上时,求出M(-2,3),M′(2,3),A(0,6),设出“孪生抛物线”把共点A(0,6)代入即可,②开口向下时,求出M(-2,-3),M′(2,-3),A(0,-6),设出“孪生抛物线”把共点A(0,-6)代入即可.
初步运用:
(1)①∵把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.
∴“孪生抛物线”的“共点”能分布在x轴上,
②∵交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”,
∴“孪生抛物线”的“共点”在y轴上,
②“孪生抛物线”y=(x-2)2-9与y=(x+2)2-9
∴令x=0,y=5,
∴共点(0,5)
故答案为×,√
(2)∵抛物线y=-2x2-4x+5=-2(x2+2x)+5=-2(x+1)2+7,
∴它的“孪生抛物线”为y=-2(x-1)2+7=-2(x2-2x+1)+7=-2x2+4x+5,
故答案为y=-2x2+4x+5;
延伸拓展:由题意得,“孪生抛物线”有下面两种情况:
①当“孪生抛物线”的开口向上时,如图1所示,
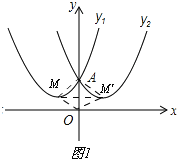
∵由于其“共点”A与M,M′,O三点恰好构成一个面积为12的菱形,且MM′=4,
∴![]() MM′×OA=12,
MM′×OA=12,
∴OA=6,
∴M(-2,3),M′(2,3),A(0,6),
由此可设“孪生抛物线”的解析式为:y=a(x+2)2+3与y=a(x-2)2+3,
∵点A(0,6)在“孪生抛物线”的图象上,
∴6=a×22+3,
∴a=![]() ,
,
∴“孪生抛物线”的解析式为:y=![]() (x+2)2+3与y=
(x+2)2+3与y=![]() (x-2)2+3;
(x-2)2+3;
②当“孪生抛物线”的开口向下时,如图2所示,
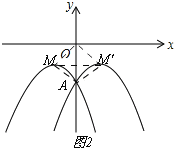
∵由于其“共点”A与M,M′,O三点恰好构成一个面积为12的菱形,且MM′=4,
∴![]() MM′×OA=12,
MM′×OA=12,
∴OA=6,
∴M(-2,-3),M′(2,-3),A(0,-6),
由此可设“孪生抛物线”的解析式为:y=a(x+2)2-3与y=a(x-2)2-3,
∵点A(0,-6)在“孪生抛物线”的图象上,
∴-6=a×22+3,
∴a=-![]() ,
,
∴“孪生抛物线”的解析式为:y=-![]() (x+2)2+3与y=-
(x+2)2+3与y=-![]() (x-2)2+3;
(x-2)2+3;


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC在射线AC上取一点D,以D为顶点、DB为一条边作∠BDF=∠A,点E在AC的延长线上,∠ECF=∠ACB
(1)如图(1),当点D在边AC上时,求证:①∠FDC=∠ABD②DB=DF
(2)如图(2),当点D在AC的延长线上时,请判断DB与DF是否相等,并说明理由

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=84°,点O是∠ABC、∠ACB角平分线的交点,点P是∠BOC、∠OCB角平分线的交点,若∠P=100°,求∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】割圆术是我国古代数学家刘徽创造的一种求周长和面积的方法:随着圆内接正多边形边数的增加,它的周长和面积越来越接近圆周长和圆面积,“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”.刘徽就是大胆地应用了以直代曲、无限趋近的思想方法求出了圆周率.请你也用这个方法求出二次函数![]() 的图象与两坐标轴所围成的图形最接近的面积是( )
的图象与两坐标轴所围成的图形最接近的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设计建造一条道路,路基的横断面为梯形ABCD,如图(单位:米).设路基高为h,两侧的坡角分别为![]() 和
和![]() ,已知h=2,
,已知h=2,![]() ,
,![]() ,
,![]() .
.
(1)求路基底部AB的宽;
(2)修筑这样的路基1000米,需要多少土石方?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 、
、![]() 、
、![]() 是常数
是常数![]() 的大致图象如图所示,抛物线交
的大致图象如图所示,抛物线交![]() 轴于点
轴于点![]() ,
,![]() .则下列说法中,正确的是( )
.则下列说法中,正确的是( )

A. abc>0 B. b-2a=0
C. 3a+c>0 D. 9a+6b+4c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,有一张三角形纸片ABC,已知∠ACB=90°,AC=24,BC=10,AB=26,点D为AB边上一点,联结CD,AD=CD=DB,沿CD把这张纸片剪成△![]() 和△
和△![]() 两个三角形如图2所示,将纸片△
两个三角形如图2所示,将纸片△![]() 沿直线
沿直线![]() 方向平移(点A、
方向平移(点A、![]() 始终都在同一直线上),
始终都在同一直线上),![]() 与
与![]() 交于点E、
交于点E、![]() 与
与![]() 、
、![]() 分别交于点E、F。
分别交于点E、F。
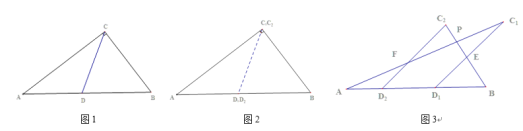
(1)在△A![]() 平移过程中,求证:
平移过程中,求证:![]()
(2)当△A![]() 平移到如图3所示的位置时,猜想图中的
平移到如图3所示的位置时,猜想图中的![]() 数量关系,并予以证明。
数量关系,并予以证明。
(3)设平移距离![]() 为x,在平移过程中,AP=
为x,在平移过程中,AP=![]() AB,PB=
AB,PB=![]() AB,请求出△APB的面积等于原△ABC面积一半时的x值。
AB,请求出△APB的面积等于原△ABC面积一半时的x值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com