
【题目】已知,如图,AD∥BC,AE平分∠BAD,点E是CD的中点.
(1)求证:AB=AD+BC
(2)求证:AE⊥BE

【答案】(1)答案见解析;(2)答案见解析.
【解析】
(1) 延长AE交BC的延长线于点F,根据角平分线和平行线的性质得到![]() ,然后等角对等边AB=BF ,再证明△FCE≌△ADE,进而等量代换求解;(2)由全等得出AE=EF,然后利用等腰三角形三线合一的性质,即可得结论;
,然后等角对等边AB=BF ,再证明△FCE≌△ADE,进而等量代换求解;(2)由全等得出AE=EF,然后利用等腰三角形三线合一的性质,即可得结论;
解:如图:延长AE交BC的延长线于点F,
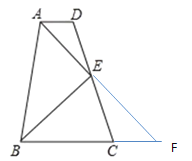
∵AE平分∠BAD
∴![]()
∵E是DC中点
∴DE=CE
∵AD∥BC
∴![]()
∴![]()
∴AB=BF
又∵在△FCE和△ADE中,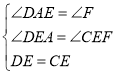
∴△FCE≌△ADE,
∴AD=CF
∴AB=BF=BC+CF=BC+AD
即AB=AD+BC
(2)由(1)可知△FCE≌△ADE
∴AE=FE
又∵BA=BF
∴根据等腰三角形三线合一的性质可知AE⊥BE.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
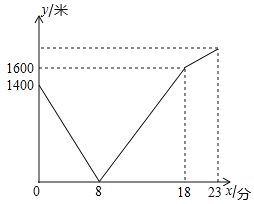
【题目】小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回![]() 两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示
![]() 妈妈从家出发______分钟后与小婷相遇;
妈妈从家出发______分钟后与小婷相遇;
![]() 相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米
相遇后妈妈回家的平均速度是每分钟______米,小婷家离学校的距离为______米![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)是燃烧时间x(h) 的一次函数.某蜡烛的高度为30cm,燃烧3h后,蜡烛剩余部分的高度为12cm.
(1)求蜡烛燃烧时y(cm)与x(h)之间的函数表达式;
(2)求出蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥BN,AE平分∠BAM,BE平分∠ABN,

(1)求∠AEB的度数.
(2)如图2,过点E的直线交射线线AM于点C,交射线BN于点D,求证:AC+BD=AB;
(3)如图3,过点E的直线交射线线AM的反向延长线于点C,交射线BN于点D,AB=5,AC=3,S△ABE﹣S△ACE=2,求△BDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义感知:我们把顶点关于![]() 轴对称,且交于
轴对称,且交于![]() 轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线
轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线![]() 与
与![]() 是一对“孪生抛物线”,其“共点”为点
是一对“孪生抛物线”,其“共点”为点![]() .
.
初步运用:
![]() 判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“
判断下列论断是否正确?正确的在题后横线上打“√”,错误的则打“![]() ”:
”:
①“孪生抛物线”的“共点”不能分布在![]() 轴上.________
轴上.________
②“孪生抛物线”![]() 与
与![]() 的“共点”坐标为
的“共点”坐标为![]() .________
.________
![]() 填空:抛物线
填空:抛物线![]() 的“孪生抛物线”的解析式为________.
的“孪生抛物线”的解析式为________.
延伸拓展:在平面直角坐标系中,记“孪生抛物线”的两顶点分别为![]() ,
,![]() ,且
,且![]() ,其“共点”
,其“共点”![]() 与
与![]() ,
,![]() ,
,![]() 三点恰好构成一个面积为
三点恰好构成一个面积为![]() 的菱形,试求该“孪生抛物线”的解析式.
的菱形,试求该“孪生抛物线”的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边中点,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F
(1)当点E在AC边上时(如图1),求证CE=BF
(2)在(1)的条件下,求证:![]()
(3)当∠EDF绕D点旋转到图3的位置即点E、F分别在AC、CB边的延长线上时,上述(2)结论是否成立?若成立,请给予证明;若不成立,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() 和
和![]() ,下列关于此二次函数的叙述,正确的是( )
,下列关于此二次函数的叙述,正确的是( )

A. 当![]() 时,
时,![]() 的值小于
的值小于![]()
B. 当![]() 时,
时,![]() 的值大于
的值大于![]()
C. 当![]() 时,
时,![]() 的值等于
的值等于![]()
D. 当![]() 时,
时,![]() 的值大于
的值大于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
(1)直线![]() 经过点C,且与x轴交与点E,求四边形AECD的面积;
经过点C,且与x轴交与点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(﹣![]() ,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移
,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移![]() 个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
个单位交轴x于点M,交直线l1于点N,求△NMF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分解因式:
(1)3x2﹣6xy+3y2
(2)﹣3x3y2+6x2y3﹣3xy4
(3)4a2﹣25b2
(4)(2x+3y)(2x﹣y)﹣y(2x﹣y)
(5)x3﹣4x
(6)(m+1)(m﹣9)+8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com