
����Ŀ��������ABCD�ı߳�Ϊ4����������������ƽ��ֱ������ϵ�У�ʹAB������X����������ϣ���A��������ǣ�1��0����
��1��ֱ��![]() ������C������x�ύ���E�����ı���AECD�������
������C������x�ύ���E�����ı���AECD�������
��2����ֱ��l������E���ҽ�������ABCD�ֳ������ȵ������֣���ֱ��l�Ľ���ʽ��
��3����ֱ��l1������F����![]() ��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��
��0��������ֱ��y=3xƽ�У�����2����ֱ��l����y������ƽ��![]() ����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������
����λ����x�ڵ�M����ֱ��l1�ڵ�N������NMF�������

���𰸡���1���ı���AECD�����Ϊ10����2��ֱ��l�Ľ���ʽΪy=2x-4����3��![]()
�������������������1��������֪�߳��Ѿ����ߣ������ı��ε������
��2��ֱ��l������E�ҽ�������ABCD�ֳ������ȵ������֣�����DC���ڵ�F�����������ε����ʣ������F�����꣬��ֱ��l�Ľ���ʽ��y=kx+b����E��F��������뼴���������ʽ��
��3������ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
��0������ֱ��y=3xƽ�У�֪k=3����F��������뼴�����b��ֵ���ɵó�ֱ��11��ͬ���������ʽy=2x-3����һ�����M��N�����꣬���������ε������ʽ���������MNF�������
�����������1����y=![]() x
x![]() ����y=4����
����y=4����![]() x
x![]() =4����ã�x=5����B�������ǣ�5��0����
=4����ã�x=5����B�������ǣ�5��0����
��y=0����![]() x
x![]() =0����ã�x=2����E�������ǣ�2��0����
=0����ã�x=2����E�������ǣ�2��0����
��OB=5��OE=2��BE=OB��OA=5��2=3����AE=AB��BE=4��3=1��
�ı���AECD�����=![]() ��AE+CD��AD=
��AE+CD��AD=![]() ��4+1����4=10��
��4+1����4=10��
��2��������E�ҽ�������ABCD�ֳ������ȵ������֣���ֱ����CD�Ľ���F������CF=AE=1����F�������ǣ�4��4����
��ֱ�ߵĽ���ʽ��y=kx+b����![]() ����ã�
����ã� ![]() ��
��
��ֱ��l�Ľ���ʽ�ǣ�y=2x��4��
��3����ֱ��l1������F����![]() ��0������ֱ��y=3xƽ�У�
��0������ֱ��y=3xƽ�У�
��ֱ��11�Ľ���ʽ��y1=kx+b����k=3��
����ã�0=3������![]() ��+b����ã�b=
��+b����ã�b=![]() ��
��
��y1=3x+![]() ��
��
��֪����2����ֱ��l����y������ƽ��![]() ����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+
����λ�������õ�ֱ�ߵĽ���ʽ��y=2x��4+![]() ��
��
����y=2x��3![]() ����y=0ʱ��x=
����y=0ʱ��x=![]() ����M��
����M��![]() ��0����
��0����
�ⷽ���� �ã�
�ã� 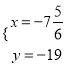 ������N����7
������N����7![]() ����19����
����19����
S��NMF=![]() ��[
��[![]() ������
������![]() ��]��|��19|=
��]��|��19|=![]() ��
��
����NMF�������![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��B��E��C��F��һ��ֱ���ϣ�AB=DF��AC=DE����A=��D��
��1����֤��AC��DE��
��2����BF=13��EC=5����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
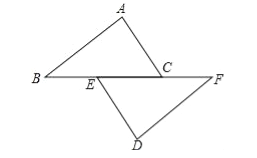
����Ŀ�����̲ı�ʽ�⣩����ֱ��ͬһ��ֱ�ߵ���ֱ��ƽ�С���������һ���ʿ���˵���������컥��ƽ�еĵ����� ��ͼ��ʾ����֪��2��ֱ�ǣ��ٶ�������1���3�ͻ�֪������ƽ�в�ƽ�У�
[���]
����һ�������á�3=90�㣬��ϡ�2�����˵�����ɣ�
�������������á�1=90�㣬��ϡ�2�����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ����2x2-2xy2��-[��-3x2y2+3x2y��+��3x2y2-3xy2��]������x=-1��y=2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʽ��x2+2x+k��һ����ȫƽ��ʽ����k��ֵ����Ϊ��������
A. 1 B. ��1 C. ��1 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
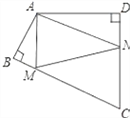
����Ŀ����ͼ���ı���ABCD�У���BAD=110�㣬��B=��D=90������BC��CD�Ϸֱ���һ��M��N��ʹ��AMN�ܳ���Сʱ�����AMN+��ANM�Ķ���Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y=ax2+bx+c��a��0����ͼ����x�����������A��x1��0����B��x2��0���������ߵĶ���ΪC����Ȼ��ABCΪ���������Σ�
��1������ABCΪ����ֱ��������ʱ����b2��4ac��ֵ��
��2������ABCΪ�ȱ�������ʱ����b2��4ac��ֵ��
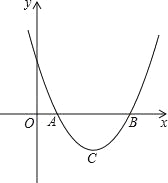
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com