练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

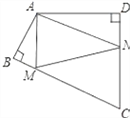
    【题目】如图，四边形ABCD中，∠BAD=110°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为_______．

    【答案】140°

    【解析】作A关于BC和CD的对称点A′，A″，连接A′A″，交BC于M，交CD于N，则A′A″即为△AMN的周长最小值。作DA延长线AH，

    ∵∠DAB=110°，

    ∴∠HAA′=70°，

    ∴∠AA′M+∠A″=∠HAA′=70°，

    ∵∠MA′A=∠MAA′，∠NAD=∠A″，且∠MA′A+∠MAA′=∠AMN，∠NAD+∠A″=∠ANM，

    ∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×70°=140°.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】对于四舍五入得到的近似数1.50万，下列说法中正确的是（（　　）

    A. 该近似数精确到百分位 B. 该近似数精确到千位 C. 该近似数精确到十分位 D. 该近似数精确到百位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正方形ABCD的边长为4，将此正方形置于平面直角坐标系中，使AB边落在X轴的正半轴上，且A点的坐标是（1，0）．

    （1）直线经过点C，且与x轴交与点E，求四边形AECD的面积；

    （2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；

    （3）若直线l1经过点F（﹣，0），且与直线y=3x平行，将（2）中直线l沿着y轴向上平移个单位交轴x于点M，交直线l1于点N，求△NMF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知⊙O1和⊙O2相交，圆心距d＝5，⊙O1的半径为3，那么⊙O2的半径r的取值范围是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】分解因式：ax2﹣4axy+4ay2= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,问CE与DF的位置关系？试说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，后求值：[（2xy﹣1）（1﹣2xy）+1]÷4xy，其中x=1，y=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据国家统计局数据，2018年全年国内生产总值为90.3万亿，比2017年增长6.6%．假设国内生产总值的年增长率保持不变，则国内生产总值首次突破100万亿的年份是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

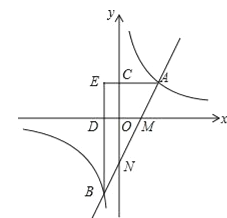
    【题目】如图，直线y=2x﹣2分别与x轴、y轴相交于M，N两点，并且与双曲线y=（k＞0）相交于A，B两点，过点A作AC⊥y轴于点C，过点B作BD⊥x轴于点D，AC与BD的延长线交于点E（m，n）．

    （1）求证：；

    （2）若，求＞2x﹣2的x的取值范围；

    （3）在（2）的条件下，P为双曲线上一点，以OB，OP为邻边作平行四边形，且平行四边形的周长最小，求第四个顶点Q的坐标．

    查看答案和解析>>

    同步练习册答案