
【题目】如图,直线y=2x﹣2分别与x轴、y轴相交于M,N两点,并且与双曲线y=![]() (k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() >2x﹣2的x的取值范围;
>2x﹣2的x的取值范围;
(3)在(2)的条件下,P为双曲线上一点,以OB,OP为邻边作平行四边形,且平行四边形的周长最小,求第四个顶点Q的坐标.
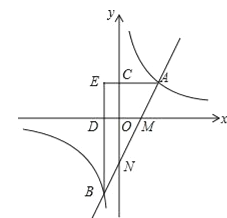
【答案】(1)、证明过程见解析;(2)、x<﹣1或0<x<2;(3)、P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).
【解析】
试题分析:(1)、设A(x1,![]() ),B(x2,
),B(x2,![]() ),则有AE=x1﹣x2,BE=
),则有AE=x1﹣x2,BE=![]() ﹣
﹣![]() ,EC=﹣x2,ED=
,EC=﹣x2,ED=![]() ,首先证明
,首先证明![]() =
=![]() ,由此即可解决问题.(2)、由DM∥AE,得
,由此即可解决问题.(2)、由DM∥AE,得![]() =
=![]() =
=![]() ,设A(m,n)则B(﹣
,设A(m,n)则B(﹣![]() ,﹣2n),把A、B代入y=2x﹣2得到:
,﹣2n),把A、B代入y=2x﹣2得到:![]() ,解得:
,解得:![]() ,求出A、B两点坐标即可解决问题.(3)、因为点B是定点,OB是定长,所以要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可,由P在y=
,求出A、B两点坐标即可解决问题.(3)、因为点B是定点,OB是定长,所以要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可,由P在y=![]() 上,设P(a,
上,设P(a,![]() ),因为OP2=n2+
),因为OP2=n2+![]() =(n﹣
=(n﹣![]() )2+8,所以当n﹣
)2+8,所以当n﹣![]() =0时,OP2的值最小,由此即可解决问题.
=0时,OP2的值最小,由此即可解决问题.
试题解析:(1)、设A(x1,![]() ),B(x2,
),B(x2,![]() ),则有AE=x1﹣x2,BE=
),则有AE=x1﹣x2,BE=![]() ﹣
﹣![]() ,EC=﹣x2,ED=
,EC=﹣x2,ED=![]() ,
,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() .
.
(2)、∵DM∥AE, ∴![]() , ∴A(m,n)则B(﹣
, ∴A(m,n)则B(﹣![]() ,﹣2n),
,﹣2n),
把A、B代入y=2x﹣2得到![]() , 解得
, 解得![]() , ∴A(2,2),B(﹣1,﹣4),
, ∴A(2,2),B(﹣1,﹣4),
由图象可知,![]() >2x﹣2时,x<﹣1或0<x<2.
>2x﹣2时,x<﹣1或0<x<2.
(3)、由(2)可知反比例函数解析式为y=![]() ,A(2,2),B(1,﹣4), ∵四边形OBPQ是平行四边形,
,A(2,2),B(1,﹣4), ∵四边形OBPQ是平行四边形,
∴OB=PQ,PO=BQ, ∵点B是定点,∴OB是定长, ∴要求平行四边形OBPQ的周长的最小值只需要求出OP的最小值即可, ∵P在y=![]() 上,设P(a,
上,设P(a,![]() ), ∴OP2=n2+
), ∴OP2=n2+![]() =(n﹣
=(n﹣![]() )2+8,
)2+8,
∴当n﹣![]() =0时,OP2的值最小, ∴n=±2时,OP有最小值, ∴P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).
=0时,OP2的值最小, ∴n=±2时,OP有最小值, ∴P(2,2)或(﹣2,﹣2),Q(1,﹣2)或(﹣3,﹣6).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
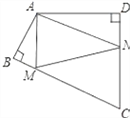
【题目】如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
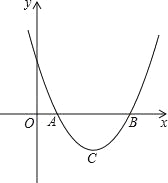
【题目】设二次函数y=ax2+bx+c(a>0)的图象与x轴的两个交点A(x1,0),B(x2,0),抛物线的顶点为C,显然△ABC为等腰三角形.
(1)当△ABC为等腰直角三角形时,求b2﹣4ac的值;
(2)当△ABC为等边三角形时,求b2﹣4ac的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 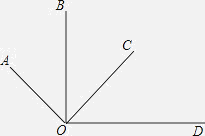
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在共有15人参加的“我爱祖国”演讲比赛中,参赛选手要想知道自己是否能进入前8名,只需要了解自己的成绩以及全部成绩的( )
A. 平均数 B. 众数 C. 中位数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于抛物线y=x2﹣4x+4,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.对称轴是直线线x=2
D.当x>2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】挑战自我!
下图是由一些火柴棒搭成的图案: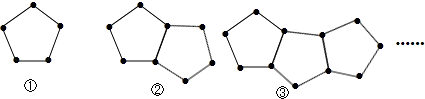
(1)摆第①个图案用几根火柴棒,
摆第②个图案用几根火柴棒,
摆第③个图案用几根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形CEFG是两个正方形,边长分别为a、b.其中B、C、E在一条直线上,G在线段CD上.三角形AGE的面积为S.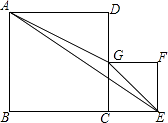
(1)①当a=5,b=3时,求S的值;
②当a=7,b=3时,求S的值;
(2)从以上结果中,请你猜想S与a、b中的哪个量有关?用字母a,b表示S,并对你的猜想进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com