
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 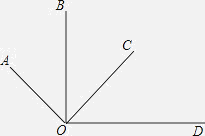
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
【答案】C
【解析】由题意可知,OA⊥OC,所以∠AOC=90°,即∠AOB+∠BOC=90°.同时,OB⊥OD,所以∠BOD=90°,即∠COD+∠BOC=90°.依次,可以判定∠AOB=∠COD,所以①正确.又因为不能推断出∠AOB与∠COD的具体角度,所以②不正确.∠AOD=∠AOB+∠BOC+∠COD,所以∠BOC+∠AOD=∠BOC+∠AOB+∠BOC+∠COD=90°+90°=180°.因为∠AOB=∠COD,所以∠AOC-∠COD=∠AOC-∠AOB=∠BOC,所以④正确.为此,选C.
【考点精析】解答此题的关键在于理解垂线的性质的相关知识,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短.


科目:初中数学 来源: 题型:
【题目】据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )
A. ﹣1≤x<6 B. ﹣1≤x≤6 C. x=﹣1或x=6 D. ﹣1<x≤6
查看答案和解析>>
科目:初中数学 来源: 题型:
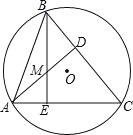
【题目】如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
A.2![]() B.2
B.2![]() C.4
C.4![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
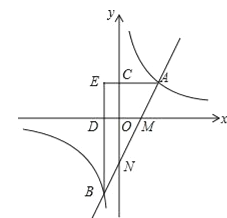
【题目】如图,直线y=2x﹣2分别与x轴、y轴相交于M,N两点,并且与双曲线y=![]() (k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(k>0)相交于A,B两点,过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,AC与BD的延长线交于点E(m,n).
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() >2x﹣2的x的取值范围;
>2x﹣2的x的取值范围;
(3)在(2)的条件下,P为双曲线上一点,以OB,OP为邻边作平行四边形,且平行四边形的周长最小,求第四个顶点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
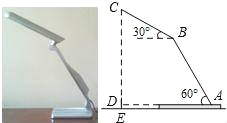
【题目】如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上星期我市某水果价格呈上升趋势,某超市第一次用1000元购进的这种水果很快卖完,第二次又用960元购进该水果,但第二次每千克的进价是第一次进价的1.2倍,购进数量比第一次少了20千克.
(1)求第一次购进这种水果每千克的进价是多少元?
(2)本星期受天气影响,批发市场这种水果的数量有所减少.该超市所购进的数量比上星期所进购的总量减少了4a%,每千克的进价在上星期第二次进价的基础上上涨5a%,结果本星期进货总额比上星期进货总额少16元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com