
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

【答案】(1)当点D在BC的中点上时,DE=DF,证明见解析;(2)有3对全等三角形,有△BED≌△CFD,△ADB≌△ADC,△AED≌△AFD;(3)CG=DE+DF,证明见解析.
【解析】试题分析:(1)因为当△BED和△CFD时,DE=DF,所以当点D在BC中点时,可利用AAS判定△BED和△CFD全等,利用全等三角形的性质可得DE=DF,
(2)在(1)的结论下:DE=DF,BD=CD, 利用SSS可判定△ADB≌△ADC,
利用HL可判定△AED≌△AFD,利用AAS可判定△BED≌△CFD,所以有3对全等三角形.
(3)连接AD,根据三角形的面积公式即可求证.
(1)当点D在BC的中点上时,DE=DF,
证明:∵D为BC中点,
∴BD=CD,
∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°,
∵在△BED和CFD中,
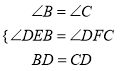
∴△BED≌△CFD(AAS),
∴DE=DF.
(2)
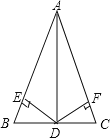
有3对全等三角形,有△BED≌△CFD,△ADB≌△ADC,△AED≌△AFD,
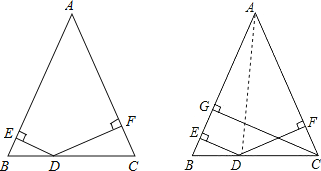
(3)CG=DE+DF,
证明:连接AD,
因为![]() ,
,
所以![]() ,
,
因为AB=AC,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)求C、D两点坐标及△BCD的面积;
(3)若点P在x轴上方的抛物线上,满足S△PCD=![]() S△BCD,求点P的坐标.
S△BCD,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
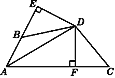
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 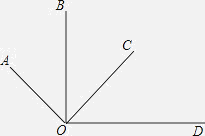
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
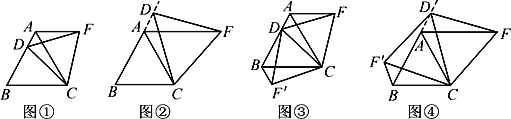
【题目】(1)操作发现:如图①,D是等边△ABC的边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,你能发现AF与BD之间的数量关系吗?并证明你发现的结论;
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与B不重合),连接DC,以DC为边在BC上方和下方分别作等边△DCF和等边△DCF′,连接AF,BF′,探究AF,BF′与AB有何数量关系?并证明你的探究的结论;Ⅱ.如图④,当动点D在等边△ABC的边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于抛物线y=x2﹣4x+4,下列说法错误的是( )
A.开口向上
B.与x轴有两个交点
C.对称轴是直线线x=2
D.当x>2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC. 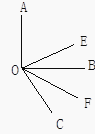
(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,…依次继续下去 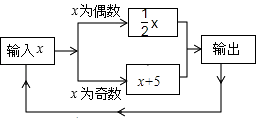
(1)请列式计算第3次到第8次的输出结果;
(2)你根据(1)中所得的结果找到了规律吗?计算2013次输出的结果是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com