
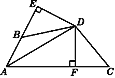
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
【答案】(1)证明见解析;(2)AB+AC=2AE.证明见解析.
【解析】试题分析:(1)、根据垂直得出△BDE与△CDE均为直角三角形,然后根据BD=CD,BE=CF得出三角形全等,从而得出DE=DF,根据角平分线的逆定理得出答案;(2)、根据角平分线得出∠EAD=∠CAD,结合∠E=∠AFD=90°得出∠ADE=∠ADF,从而说明△AED≌△AFD,根据全等得出AE=AF,最后根据AB+AC=AE﹣BE+AF+CF得出答案.
试题解析:(1)、∵DE⊥AB于E,DF⊥AC于F, ∴∠E=∠DFC=90°,∴△BDE与△CDE均为直角三角形,
∵![]() ,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
,∴△BDE≌△CDF, ∴DE=DF,即AD平分∠BAC;
、AB+AC=2AE.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】如图,P是抛物线y=2(x﹣2)2对称轴上的一个动点,直线x=t平行y轴,分别与y=x、抛物线交于点A、B.若△ABP是以点A或点B为直角顶点的等腰直角三角形,求满足条件的t的值,则t= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要6300万美元,“6300万”用科学记数法可表示为( )
A.6.3×103B.6.3×104C.6.3×107D.6.3×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当式子|x+1|+|x﹣6|取得最小值时,x的取值范围为( )
A. ﹣1≤x<6 B. ﹣1≤x≤6 C. x=﹣1或x=6 D. ﹣1<x≤6
查看答案和解析>>
科目:初中数学 来源: 题型:
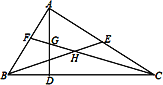
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
① △ABE的面积与△BCE的面积相等;② ∠AFG=∠AGF;③ ∠FAG=2∠ACF;④ BH=CH
A. ①②③ B. ②③④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB、AC引垂线,垂足分别为E、F点.
(1)当点D在BC的什么位置时,DE=DF?并证明.
(2)在满足第一问的条件下,连接AD,此时图中共有几对全等三角形?并请给予写出(不 必证明).
(3)过C点作AB边上的高CG,请问DE、DF、CG的长之间存在怎样的等量关系?并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
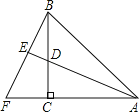
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BF⊥AD,AD的延长线交BF于E,且E为垂足,则结论①AD=BF,②CF=CD,③AC+CD=AB,④BE=CF,⑤BF=2BE,其中正确的结论的个数是( )
A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自1939年创办以来,重庆育才中学一直坚守文化底线,不断挑战自我极限,在沧桑文化中愈加根深叶茂.在今年,即将推出的本部改造计划不仅是文化审美层面的颠覆尝试,也是学校发展的巨大工程,其中三种style的民国大门各具特色,A磅礴大气,B清爽简约,C典雅古朴款,为调查民意学校让教职工进行投票呈现了四种结果,喜欢A款、喜欢B款、喜欢C款、都可以,现调查结果如下:
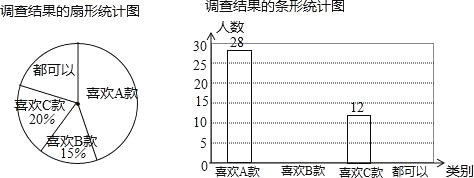
(1)如图,喜欢C款的占20%,喜欢B款的占15%,则调查总人数为,扇形统计图中认为“都可以”的所占圆心角为度;根据题中信息补全条形统计图.
(2)我们学校共有600名教职工,请根据上图估算喜欢A款的有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com